3.Вычисляют с контролем (2 контроль)

(2.9)

4. Определяют средние квадратические ошибки.

а) ошибку единицы веса по формуле Бесселя:

(2.10)

б) среднюю квадратичную ошибку среднего весового:

; (2.11)

в) среднюю квадратичную ошибку ошибки единицы веса:

; (2.12)

г) среднюю квадратичную ошибку средней квадратичной ошибки среднего весового:

(2.13)

5.Определяют доверительные интервалы для:

а) математического ожидания измерения

(2.14)

где параметр t_β выбирают из таблиц распределения Сьюдента (например, приложение V в [1] или приложения (2) ) по заданной доверительной вероятности β и числу степеней свободы ;

б) дисперсии единицы веса:

(2.15)

в) среднего квадратичного отклонения среднего весового:

(2.16)

где μ и М средние квадратические ошибки, вычисленные по формулам (2.10) и (2.11). Коэффициенты γ₁ и γ ₂ выбирают из специальных таблиц по доверительной вероятности и по числу степеней свободы (приложение VIII в [l] или приложение (3) ).

Пример. Приведенные результаты измерений превышений и длины семи секций нивелирования, последние выражены в км. По результатам измерений выполнить обработку ряда неравноточных измерений. Доверительные оценки получить с вероятностью 0,95.

Принимаем =3,120м

По формулам (2.3 – 2.13) вычисляем:

- общую арифметическую средину (среднее весовое)

- среднюю квадратическую ошибку единицы веса:

- среднюю квадратическую ошибку ошибки единицы веса:

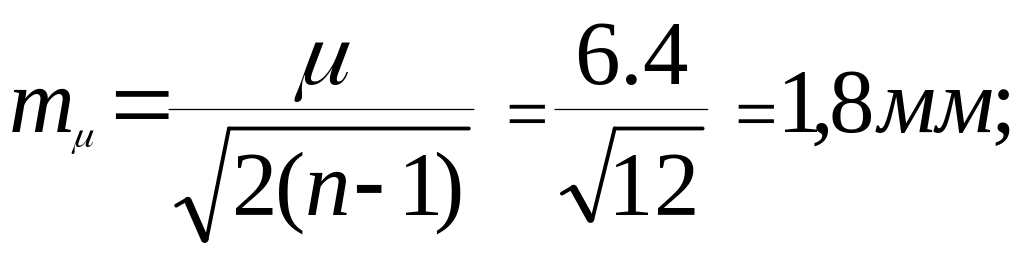
- среднюю квадратическую ошибку общей арифметической средины (среднего весового):

- среднюю квадратическую ошибку средней квадратичной ошибки общей арифметической средины:

Сравним значения средних квадратических ошибок μ и M, и их средних квадратических ошибок m_μ и m_M. Из сравнения видно, что при исчислении средних квадратических ошибок достаточно оставлять две значащие цифры, при этом вторая цифра уже неточна.

Необходимые промежуточные вычисления и контроли приведены в таблице 2.1.

Таблица 2.1

№	Превышение hi,м	Длина хода Li, км	Вес Рi	εi мм	Рεi мм	рεi2 мм2	vi мм	рvi мм	рvi2 мм2	Контроль
1	3,117	1,083	0,92	-3	-2,77	8,310	-8,05	-7,436	59,8806
2	3,126	0,956	1,05	6	6,28	37,657	0,95	0,991	0,9381	1контроль
3	3,135	1,066	0,94	15	14,07	211,069	9,95	9,331	92,8171	<0.03
4	3,130	1,250	0,80	10	8,00	80,000	4,95	3,958	19,5783	2контроль
5	3,119	0,752	1,33	-1	-1,33	1,330	-6,05	-8,049	48,7217	243,1031= 243,103
6	3,122	1,963	0,51	2	1,02	2,038	-3,05	-1,555	4,7482
7	3,131	2,154	0,46	11	5,11	56,175	5,95	2,761	16,4192
Σ			6,01		30,37	396,579		0,000	243,103

Строим доверительные интервалы:

а) доверительный интервал для математического ожидания измеренной величины. Значение t_β найдем по доверительной вероятности β = 0,95 по числу степеней свободы k = 7-1 = 6, по таблицам распределения Сьюдента из приложения (2), tβ = 2,6.

3,125м - 2,6 * 2,6мм< < 3,125м + 2,6 * 2,6мм

или

3,1182м< < 3,1318м

б) дисперсии единицы веса

Значения. γ1 и γ 2 найдем по доверительной вероятностью β = 0,95 и по числу степеней свободы k = 7-1 = 6, из таблиц приложения (3). Значения γ₁ = 0,644 и γ ₂ = 2,202.

6,7мм * 0,644 < < 6,7мм* 2,202,

или

28,9мм² < < 98,4мм²

в) среднего квадратичного отклонения среднего весового

2,6мм * 0,644 < <2,6мм * 2,202

Или

1,67мм< 5,72мм

Вывод по работе:

Наиболее достоверным значением измеренной величины является

Его средняя квадратическая ошибка составляет

мм

Математическое ожидание измеренной величины с вероятностью 0,95 принадлежит интервалу

3,1182м< < 3,1318м