
- •Оглавление
- •Правила выполнения и оформления контрольных работ
- •Вариант 0. Контрольная работа №1 «Линейная алгебра. Аналитическая геометрия»
- •Контрольная работа №2 «Введение в анализ. Дифференциальное исчисление функции одной и нескольких переменных»
- •Вариант 1. Контрольная работа №1 «Линейная алгебра. Аналитическая геометрия»
- •Контрольная работа №2 «Введение в анализ. Дифференциальное исчисление функции одной и нескольких переменных»
- •Вариант 2. Контрольная работа №1 «Линейная алгебра. Аналитическая геометрия»
- •Контрольная работа №2 «Введение в анализ. Дифференциальное исчисление функции одной и нескольких переменных»
- •Вариант 3. Контрольная работа №1 «Линейная алгебра. Аналитическая геометрия»
- •Контрольная работа №2 «Введение в анализ. Дифференциальное исчисление функции одной и нескольких переменных»
- •Вариант 4. Контрольная работа №1 «Линейная алгебра. Аналитическая геометрия»
- •Контрольная работа №2 «Введение в анализ. Дифференциальное исчисление функции одной и нескольких переменных»
- •Вариант 5. Контрольная работа №1 «Линейная алгебра. Аналитическая геометрия»
- •Контрольная работа №2 «Введение в анализ. Дифференциальное исчисление функции одной и нескольких переменных»
- •Вариант 6. Контрольная работа №1 «Линейная алгебра. Аналитическая геометрия»
- •Контрольная работа №2 «Введение в анализ. Дифференциальное исчисление функции одной и нескольких переменных»
- •Контрольная работа №1 «Линейная алгебра. Аналитическая геометрия»
- •Контрольная работа №2 «Введение в анализ. Дифференциальное исчисление функции одной и нескольких переменных»
- •Вариант 8. Контрольная работа №1 «Линейная алгебра. Аналитическая геометрия»
- •Контрольная работа №2 «Введение в анализ. Дифференциальное исчисление функции одной и нескольких переменных»
- •Вариант 9. Контрольная работа №1 «Линейная алгебра. Аналитическая геометрия»
- •Контрольная работа №2 «Введение в анализ. Дифференциальное исчисление функции одной и нескольких переменных»
- •Типовой разбор варианта контрольной работы
- •Контрольная работа №1
- •Контрольная работа №2
- •Список рекомендуемой литературы.
- •Вопросы к экзамену по математике.
Контрольная работа №2 «Введение в анализ. Дифференциальное исчисление функции одной и нескольких переменных»
1) Вычислить пределы, не пользуясь правилом Лопиталя:
a)
![]() ;
b)
;
b)
![]() ;
c)
;
c)
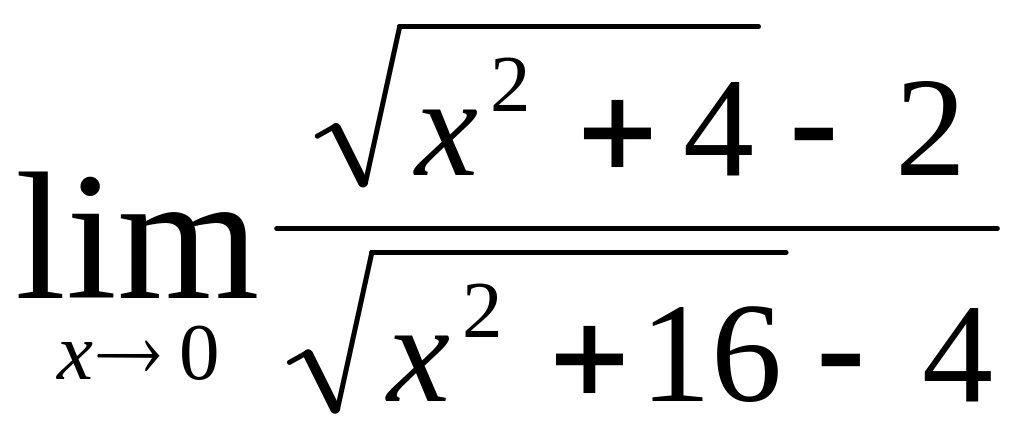 ;
;
d)
![]() ;
e)
;
e)
![]()
2)Исследовать функции на непрерывность. Классифицировать точки разрыва.
a)
![]() ;
b)
;
b)
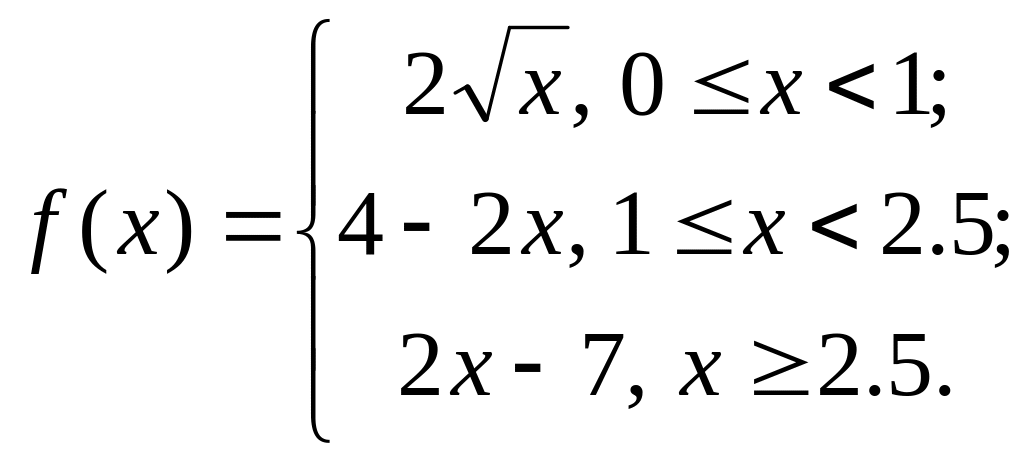
3) Найти производные для следующих функций:
a)
![]() ;
b)
;
b)
![]() ;
c)
;
c)
![]() ;
d)
;
d)
![]()
4) Найти уравнения
касательной и нормали к графику функции
![]()
в точке x0=-1.
5) С помощью методов
дифференциального исчисления построить
график функции
![]() .
.
6) Найти наибольшее
и наименьшее значения функции
![]()
на отрезке
![]() .
.
7) Даны функция
![]() и точки A(3;2),
B(2,97;2,02).
Вычислить:
и точки A(3;2),
B(2,97;2,02).
Вычислить:
a)значение функции ;
b) с помощью дифференциала, заменяя приращение при переходе от A к B дифференциалом. Оценить в процентах относительную погрешность вычисления.
c) cоставить уравнения касательной плоскости и нормали к поверхности в точке A.
8) Даны функция
![]() ,
точка М(1;2;-1) и вектор
,
точка М(1;2;-1) и вектор
![]() .
.
Найти:
a) градиент данной функции в точке М;
b) производную функции в точке М по направлению вектора .
9) Дана функция
![]() .
Найти:
.
Найти:
a) экстремум данной функции;
b) наибольшее и наименьшее значения функции в области , ограниченной линиями:
Вариант 2. Контрольная работа №1 «Линейная алгебра. Аналитическая геометрия»
1) Даны матрицы:
![]() ,
,
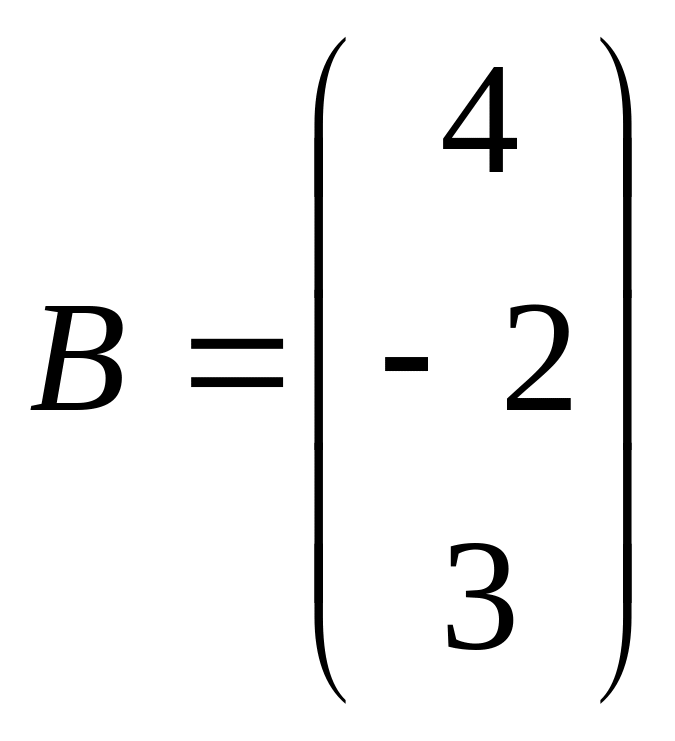 ,
,
![]() ,
,
![]() .
.
Найти
![]()
2) Дана матрица
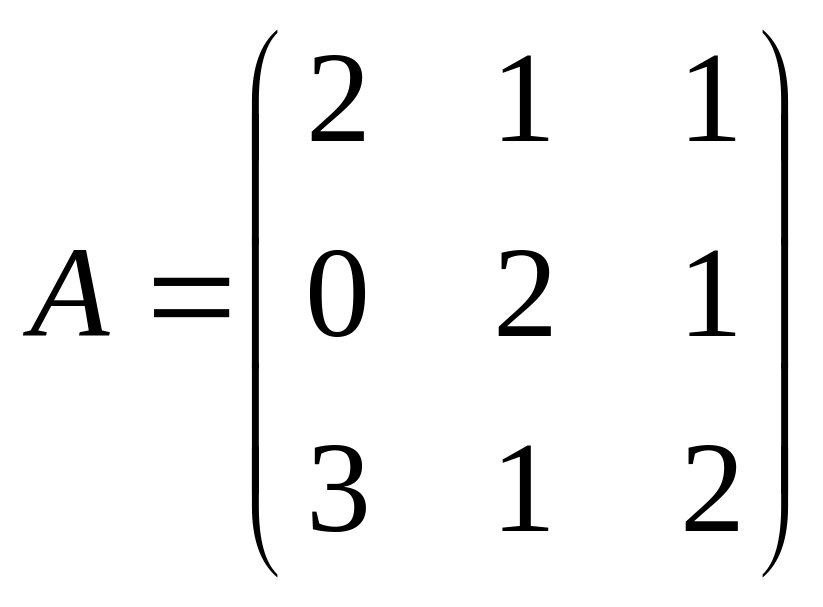 .
Найти обратную к ней матрицу
.
Найти обратную к ней матрицу
3) Решить системы линейных уравнений методом Жордана – Гаусса:
а)
![]() b)
b)
![]()
4) Даны
векторы
![]() .
.
a)Доказать, что вектора образуют базис и найти разложение вектора по этому базису.
b) Найти скалярное произведение векторов и .
c) Найти векторное произведение векторов и .
d) Найти смешанное произведение векторов .
5) Даны координаты вершин треугольника, A(3;3), B(-13;-9), C(-6;15). Найти:
a) длину стороны AB;
b) общие уравнения сторон AB и BC;
c) величину угла B;
d)длину и уравнение высоты, опущенной из вершины ;
e) площадь треугольника ;
f) уравнение прямой, проходящей через точку параллельно стороне .
6) Даны четыре точки A(-0,5;1;2), B(-2,5;2;1), C(1,5;0;1), M(0;2;1). Найти:
a)уравнение плоскости , проходящей через три точки A, B, C;
b)каноническое уравнения прямой AB;
c)уравнение и длину высоты, опущенной из вершины М на грань ;
d) объем пирамиды АВСМ.
7) Дано
уравнение кривой второго порядка:
![]() .
.
Привести его к каноническому виду, определить вид кривой, указать её параметры (для эллипса и гиперболы – центр, вершины, полуоси, фокусы, а для гиперболы и асимптоты. Для параболы указать координаты вершины, координаты фокуса, величину параметра p, уравнение директрисы). Изобразить кривую на координатной плоскости.
Контрольная работа №2 «Введение в анализ. Дифференциальное исчисление функции одной и нескольких переменных»
1) Вычислить пределы, не пользуясь правилом Лопиталя:
a)
![]() ;
b)
;
b)
![]() ;
c)
;
c)
![]() ;
;
d)
![]() ;
e)
;
e)
![]()
2)Исследовать функции на непрерывность. Классифицировать точки разрыва.
a)
![]() ;
b)
;
b)
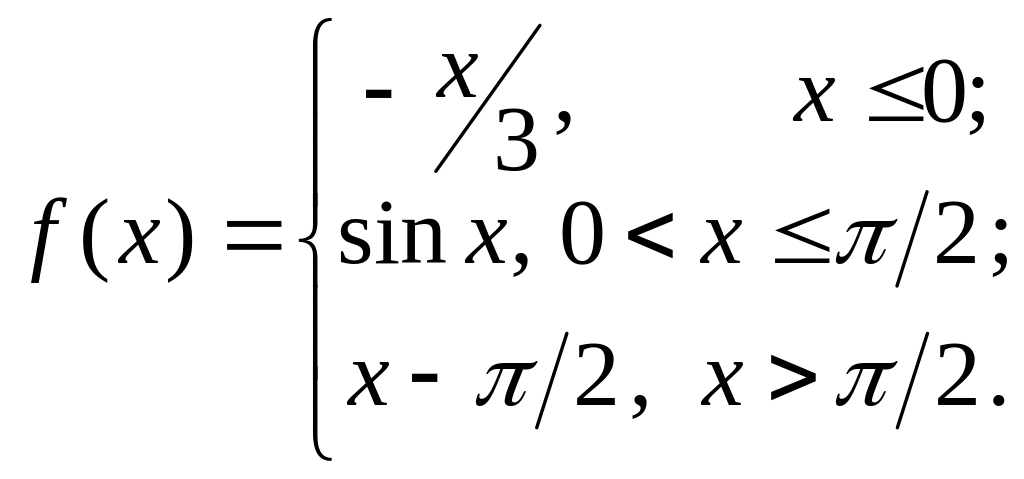
3) Найти производные для следующих функций:
a)
![]() ;
b)
;
b)
![]() ;
c)
;
c)
![]() ;
d)
;
d)
![]()
4) Найти уравнения
касательной и нормали к графику функции
![]()
в точке x0=-2.
5) С помощью методов
дифференциального исчисления построить
график функции
![]() .
.
6) Найти наибольшее
и наименьшее значения функции
![]()
на отрезке
![]() .
.
7) Даны функция
![]() и точки A(1;1),
B(0,98;1,03).
Вычислить:
и точки A(1;1),
B(0,98;1,03).
Вычислить:
a)значение функции ;
b) с помощью дифференциала, заменяя приращение при переходе от A к B дифференциалом. Оценить в процентах относительную погрешность вычисления.
c) cоставить уравнения касательной плоскости и нормали к поверхности в точке A.
8) Даны функция
![]() ,
точка М(2;2;4) и вектор
,
точка М(2;2;4) и вектор
![]() .
.
Найти:
a) градиент данной функции в точке М;
b) производную функции в точке М по направлению вектора .
9) Дана функция
![]() .
.
Найти:
a) экстремум данной функции;
b)
наибольшее и наименьшее значения функции
в области
,
ограниченной линиями:
![]()
