6.3. Электромагнитная индукция

Явление электромагнитной индукции заключается в следующем: если в пространстве существует переменное магнитное поле, то в этом же пространстве всегда существует сопутствующее ему электрическое поле, которое называют индукционным электрическим полем.

Магнитным потоком Φ (или потоком вектора магнитной индукции) через поверхность S называют величину, равную

. (6.3.1)

Из замкнутости силовых линий магнитной индукции следует, что магнитный поток через любую замкнутую поверхность равен нулю:

. (6.3.2)

Уравнение (6.3.2) устанавливает факт отсутствия в природе магнитных зарядов.

В однородном магнитном поле магнитный поток через плоскую поверхность произвольной формы S равен:

, (6.3.3)

Рис. 6.3.1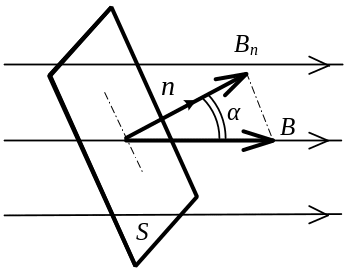

где α – угол между вектором и вектором нормали к поверхности (рис. 6.3.1).

При изменении магнитного потока через поверхность, ограниченную замкнутым проводящим контуром, в последнем появляется электрический ток. Этот ток называют индукционным. Появление тока в проводнике означает наличие электрического поля, которое двигает заряды. В случае электромагнитной индукции источником этого электрического поля является переменное магнитное поле.

Индукционное электрическое поле обладает следующими свойствами:

• работа сил индукционного поля при перемещении заряда по замкнутому контуру не равна нулю; для единичного заряда она равна циркуляции вектора напряжённости этого электрического поля, и её называют электродвижущей силой индукции (ЭДС):

; (6.3.4)

• силовые линии индукционного поля замкнуты – индукционное электрическое поле является вихревым.

Закон Фарадея: ЭДС индукции, возникающая в контуре, равна с обратным знаком скорости изменения магнитного потока через поверхность, ограниченную этим контуром:

. (6.3.5)

Знак «минус» в формуле (6.3.5) соответствует тому, что направление положительной нормали к контуру и положительное направление тока и ЭДС в контуре связаны друг с другом правилом правого винта.

Направление индукционного тока в контуре находят по правилу Ленца: индукционный ток в контуре направлен таким образом, чтобы своим магнитным полем препятствовать изменению магнитного потока, порождающего этот индукционный ток, или чтобы препятствовать причине, вызывающей появление индукционного тока.

Электрический ток силой I, протекающий по замкнутому проводнику (контуру), создает вокруг проводника магнитное поле. Это магнитное поле через поверхность, ограниченную контуром, создаёт магнитный поток прямо пропорциональный силе тока в контуре:

. (6.3.6)

Коэффициент пропорциональности L в формуле (6.3.6) называют индуктивностью контура – величиной, характеризующей магнитные свойства электрических цепей.

Индуктивность зависит от размеров и формы контура, а также от магнитных свойств среды, в которую он помещен. В частности, индуктивность соленоида длиной l и площадью поперечного сечения S равна (среда – вакуум):

, (6.3.7)

где V – объем соленоида, N – полное количество витков в соленоиде.

Самоиндукция – явление возникновения дополнительного индукционного тока в контуре при изменении основного тока, протекающего в нем. ЭДС самоиндукции равна:

. (6.3.8)

Знак "–" в формуле (6.3.8) означает, что, в соответствии с правилом Ленца, индукционный ток направлен таким образом, чтобы препятствовать изменению основного тока в контуре. Если основной ток увеличивается, то ток самоиндукции направлен в противоположную ему сторону. И наоборот, если основной ток уменьшается, то ток самоиндукции направлен в ту же сторону.

Энергия магнитного поля может быть выражена через характеристики поля – магнитную индукцию и объем пространства, в котором локализовано магнитное поле:

. (6.3.9)

Если магнитное поле создано током силой I, который идет по индуктивности L, то энергия, запасенная в магнитном поле индуктивности равна:

. (6.3.10)

Ток при замыкании и размыкании цепи: вследствие явления самоиндукции установление тока при замыкании цепи до значения , и убывание тока при её размыкании происходит не мгновенно, а по экспоненциальным законам:

и . (6.3.11)

Здесь R – сопротивление цепи. Скорость убывания тока (или возрастания) определяется величиной , которую называют постоянной времени релаксации цепи.

Уравнения Максвелла – четыре основных уравнения классической электродинамики, описывающие электромагнитные явления и в вакууме и в произвольной среде. Уравнения Максвелла для случая электрического и магнитного полей в вакууме при наличии в объеме V электрического заряда, распределенного с плотностью , и тока проводимости с плотностью j в интегральной форме имеют вид:

(6.3.12)