Частица в бесконечно глубокой потенциальной яме

Рассмотрим частицу, потенциальная энергия которой в интервале координат [0,l] равна нулю, а вне этого интервала бесконечно велика. Внутри такой потенциальной ямы стационарное уравнение Шредингера имеет вид такой же, как для свободной частицы (U=0):

(ħ²/2m) E (x) (9.4.4)

Ища решение (9.4.4) в виде осциллирующей функции , удовлетворяющей граничным условиям , можно получить, что для частицы полная энергия квантована, то есть возможен только дискретный набор полных энергий:

, n=1, 2, 3, (9.4.5)

Целое число n, нумерующее допустимые значения полной энергии называется квантовым числом. Каждому квантовому состоянию с определенным значением полной энергии E_n соответствует своя волновая функция:

(9.4.6)

Рис. 9.4.3

Первые четыре волновые функции, соответствующие уровням с n=1, 2, 3, 4, показаны на рис. 9.4.3.

Решенная выше простейшая задача отражает следующие общие свойства частицы, находящейся в потенциальной яме любой формы.

1) Частица, локализованная в потенциальной яме, может обладать только определенными дискретными значениями полной энергии E_n. Невозможно существование локализованных частиц с нулевой энергией. Состояние частицы с минимальной полной энергией называется основным состоянием.

2) Волновая функция частицы в состоянии с наименьшей полной энергией не обращается в ноль нигде в пределах потенциальной ямы. Волновые функции частицы во всех состояниях с бóльшими энергиями могут принимать нулевые значения в пределах ямы. Точки, где волновая функция обращается в ноль, называются узлами волновой функции. Количество узлов увеличивается на единицу при переходе к каждому следующему по энергии состоянию.

5. Теория атома

Атом водорода. Атомные спектры.

Первый постулат Бора  электроны могут двигаться вокруг атомного ядра, не излучая электромагнитную энергию, только по стационарным орбитам, определяемым из условия квантования момента импульса электрона:

, n = 1, 2, ... (9.5.1)

где m_е – масса электрона; υ_n – скорость электрона на n-й орбите; r_n – радиус n-й стационарной орбиты; n – номер стационарной орбиты; ħ − величина, связанная с постоянной Планка h соотношением ħ = h/ 2π, обычно также называемая постоянной Планка.

Второй постулат Бора  каждой разрешенной условием квантования электронной орбите соответствует определенное дискретное значение энергии. Переход с более удаленной от ядра орбиты на более близкую орбиту происходит скачкообразно и сопровождается испусканием кванта электромагнитного излучения.

Энергия испускаемого кванта Е, а также его частота , определяется из соотношения:

Е= Е_m  Е_n = h, (9.5.2)

где Е_m  энергия электрона на орбите m; Е_n − энергия электрона на орбите n.

Из постулатов Бора следует, что полная энергия электрона на n-й орбите атома водорода Е_n может быть рассчитана по формуле:

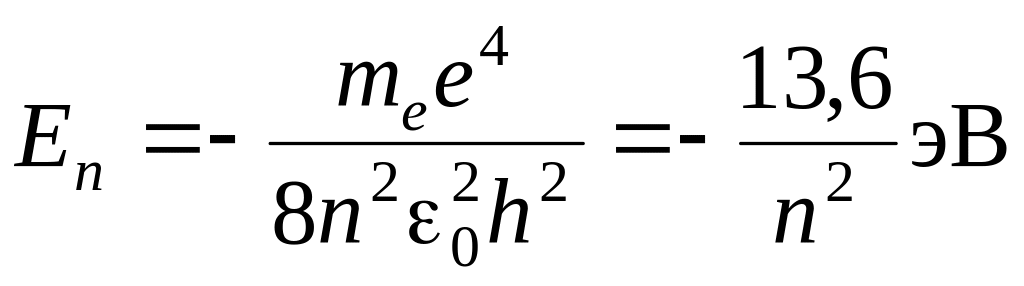, (9.5.3)

где n – номер стационарной орбиты, на которой находится электрон.

При переходе электрона с орбиты m, более удаленной от ядра, на более близкую к ядру орбиту n, согласно второму постулату Бора и выражению для полной энергии электрона на стационарной орбите, частота кванта излучения определяется соотношением:

. (9.5.4)

Это так называемая сериальная формула для спектра частот атома водорода, где R = 3,28984∙10¹⁵ Гц − постоянная величина, называемая постоянной Ридберга (полезно помнить, что hR = 13,6 эВ).

Теорию Бора можно успешно использовать не только для атома водорода, но и при рассмотрении водородоподобных атомов, т.е. ионов других химических элементов, состоящих из ядра с зарядом Ze и одного электрона (Не⁺, Li²⁺, Be³⁺, …), обладающих сходными оптическими свойствами. Так, сериальная формула для водородоподобных ионов имеет вид аналогичный сериальной формуле для водорода:

, (9.5.5)

где Z – заряд ядра в относительных единицах (при Z = 1 формула переходит в сериальную формулу для водорода).

Теория атома Бора явилась промежуточным звеном в понимании новых квантовых закономерностей физики микромира. Принципы квантования электронных орбит, предложенные Бором в его теории атома, получили дальнейшее теоретическое обоснование в квантовой механике.

Квантовые числа. Спин электрона. Принцип Паули. Бозоны и фермионы.

В квантовой механике состояние частицы задается волновой функцией (или пси-функцией) Ψ , которая является комплексной величиной, и поэтому недоступна наблюдению. Доступной эксперименту физической величиной является плотность вероятности, т.е. вероятности w нахождения частицы в единице объема, которую позволяет определить пси-функция Ψ :

. (9.5.6)

Общее уравнение Шрёдингера (основное уравнение квантовой механики):

− , (9.5.7)

где Ψ – волновая функция, описывающая нестационарное состояние частицы; Δ − оператор Лапласа; m – масса частицы;U( ) – потенциальная энергия;i − мнимая единица.

ψ-функции, в случае решения уравнения для атома водорода, содержат три целочисленных параметра − n, l, m. В квантовой механике n называют главным квантовым числом, определяющим энергию связанных состояний электрона.

Движение электрона в атоме характеризуется орбитальным моментом импульса, его модуль М_l связан с так называемым орбитальным (или азимутальным) квантовым числом: .

Орбитальное квантовое число l характеризует форму электронного облака (т.е. характер распределения по объему атома плотности вероятности появления электрона) и может принимать значения 0, 1, 2, … (п − 1).

Проекция орбитального момента на направление z равняется , при этом оказывается, что m_l также квантуется и принимает (2l+1) значение: m_l = 0, ±1, ±2, ±3, …. ±l. Число m_l называют магнитным орбитальным квантовым числом. Квантовое число m_l определяет ориентацию электронного облака в пространстве.

Кроме перечисленных выше характеристик электрона в атоме, имеется еще одна характеристика − это собственный момент импульса электрона M_s, называемый также спином. Эта величина имеет исключительно квантовую природу и не имеет классических аналогов. Величина спинового момента электрона равна , где − величина, называемая магнитным спиновым квантовым числом. Обычно это число (в единицах ħ) также называют спином.

Электронная конфигурация многоэлектронного атома.

Значения квантовых чисел n, l, m_l, m_s полностью определяют состояние электрона в одноэлектронном атоме. Подобная задача для многоэлектронных атомов может быть решена лишь приближенно, т.к. становится существенным взаимное влияние электронов друг на друга. В отличие от одноэлектронного атома, энергия электрона в многоэлектронном атоме будет зависеть не только от n, но и от l.

Распределение электронов по уровням энергии с различными n и l называют электронной конфигурацией многоэлектронного атома.

Совокупность электронов атома с одинаковыми значениями квантового числа п образует электронную оболочку. Данному значению главного квантового числа п соответствует 2п² состояний, отличающихся друг от друга значениями квантовых чисел l, m_l, m_s.

Оболочки подразделяют на подоболочки, отличающиеся квантовым числом l. Различные состояния в подоболочке отличаются значениями квантовых чисел m_l и m_s. Число состояний в подоболочке равно 2(2l + 1). Заселение подоболочек электронами происходит в соответствии с принципом Паули.

Бозоны (или бозе-частицы)  это частицы с нулевым или целочисленным спином. Бозоны подчиняются статистике Бозе − Эйнштейна (отсюда − название частиц), согласно которой в данном квантовом состоянии может находиться произвольно большое число бозонов определенного типа.

Фермионы (или ферми-частицы)  это частицы, обладающие полуцелым спином. Системы одинаковых фермионов подчиняются квантовой статистике Ферми − Дирака, сформулированной для систем тождественных (одинаковых) частиц с полуцелым спином.

Принцип Паули: в атоме не может быть электронов с одинаковыми значениями всех четырех квантовых чисел.

Испускание и поглощение света. Правило отбора для квантового числа l. Испускание и поглощение света происходит при переходах электрона в атоме с одного уровня энергии на другой. В квантовой механике доказывается, что для квантового числа l действует правило отбора, согласно которому возможны только те переходы между уровнями, при которых l изменяется на единицу: Это правило есть следствие закона сохранения момента импульса, связано с тем, что фотон, обладая моментом импульса ħ, при испускании уносит из атома этот момент, а при поглощении − привносит.