ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

Государственное образовательное учреждение

высшего профессионального образования

«УРАЛЬСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

ПУТЕЙ СООБЩЕНИЯ»

Факультет

Управление процессами перевозок

Специальность

Технология транспортных процессов

Кафедра

Станции, узлы и грузовая работа

Отчет

по лабораторным работам

Дисциплина: Математическое моделирование в профессиональной деятельности

Работу выполнила

студентка группы №	116-ТТПмз				Поспелова Е.В.
			подпись, дата		инициалы, фамилия

Работу принял

профессор				Казанцева Н.В.
должность, уч. степень, звание		подпись, дата		инициалы, фамилия

Екатеринбург

2017

Оглавление

Лабораторная работа №1. Интерполяция 3

1. Постановка задачи 3

2. Математическое описание 3

3. Описание результатов решения задач в MathCAD 4

4. Анализ полученных результатов и выводы 5

Лабораторная работа №2. Аппроксимация экспериментальных зависимостей 6

1. Постановка задачи 6

2. Математическое описание 6

3. Описание результатов решения задач в MS Excel 8

4. Анализ полученных результатов и выводы 10

Лабораторная работа №3. Численное интегрирование 11

1. Постановка задачи 11

2. Математическое описание 11

3. Описание результатов решения задач в MathCAD 13

4. Анализ полученных результатов и выводы 14

Лабораторная работа №4. Транспортная задача 15

1. Постановка задачи 15

2. Математическое описание 15

3. Описание результатов решения задач в MS Excel 18

4. Анализ полученных результатов и выводы 19

Лабораторная работа №5. Численное решение дифференциальных уравнений 21

1. Постановка задачи 21

2. Математическое описание 21

3. Описание результатов решения задач в MathCAD 23

4. Анализ полученных результатов и выводы 24

Лабораторная работа №1. Интерполяция

Вариант 2

1. Постановка задачи

Построить интерполяционный кубический сплайн для функции y=f(x), заданной таблицей. Используя найденную зависимость, найти значение у в точке x = N + 0.55 , где N – номер варианта.

2	2,1	2,2	2,3	2,4	2,5	2,6	2,7	2,8	2,9	3
2,312	2,251	2,418	2,752	2,7	2,459	3,022	3,079	2,42	2,669	3,241

2. Математическое описание

В большинстве практических приложений желательно соединить экспериментальные точки не ломаной линией, а гладкой кривой.

Лучше всего для этих целей подходит интерполяция сплайнами, т. е. фрагментами полиномов. Смысл сплайн-интерполяции заключается в том, что в каждом промежутке между узловыми точками (на каждом шаге интерполяции) осуществляется аппроксимация в виде определенной полиномиальной зависимости f(x). При этом для каждого шага получается свой полином, причем его коэффициенты подбираются такими, чтобы на границах шага выполнялись условия сшивки. А именно, если применяются сплайны в виде полиномов степени m, то несложно показать, что их коэффициенты можно выбрать так, чтобы обеспечить непрерывность производных порядка до (m-1)-й включительно.

Наиболее часто применяются кубические сплайны, т.е. полиномы третьей степени (кубические параболы):

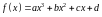
Коэффициенты a,b,c,d рассчитываются независимо для каждого промежутка интерполирования, исходя из значений y_i в соседних точках. Участки парабол называются кубическими сплайнами.

Приведем формулы для расчета кубической сплайн-интерполяции. Искомая функция на промежутке между x_i и x_i+1 вычисляется следующим образом:

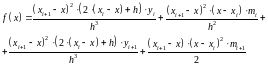
где

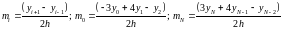
Источник: Турчак, Л.И. Основы численных методов. / Л.И.Турчак – М.: Наука, 1987. – с. 51-53