тип 3	регулярные
	леволинейная	AB | , где A,BVN , VT*
	праволинейная	AB | , где A,BVN , VT*.
тип 3	автоматные
	леволинейная	ABt | t, где A,BVN , tVT
	праволинейная	AtB | t, где A,BVN , tVT

Моделировать работу ДКА значительно проще, чем НКА. Доказано, что для любого НКА можно построить эквивалентный ему ДКА. Для этого существует специальный алгоритм, идея которого состоит в следующем:

• В качестве состояний нового ДКА рассматриваются все состояния исходного автомата, а также всевозможные сочетания этих состояний по два, по три, …, по n, если в исходном автомате было n состояний.

• Для всех новых состояний строится функция переходов, в которой для каждого состояния q_iq_j появляется переход в новое состояние, представляющий собой объединение всех прежних переходов из q_i и q_j.

• Начальное состояние нового автомата остается тем же, а множество конечных состояний нового автомата будут состоять из всех сочетаний, в которых присутствовало q_f – конечное состояние исходного автомата.

После построения ДКА из него удаляют все недостижимые состояния (состояния, переход в которые невозможен при любой входной цепочке).

В итоге построен ДКА, эквивалентный заданному НКА. При этом если исходный автомат имел n состояний, то в наихудшем случае построенный ДКА будет иметь (2ⁿ–1) состояний.

Рассмотрим на примере построение ДКА, эквивалентного заданному НКА.

1. Пусть M=({p,q,r},{0,1},,p,{r}) – НКА, где функция переходов  задана графом:

Недетерминированный автомат M допускает все цепочки из {0,1}*, заканчивающиеся двумя единицами: (0+1)*11. Представим функцию переходов в табличном виде (таблица справа).						вход
					состояние	0	1
					p	{p}	{p,q}
					q	–	{r}
					r	–	–
	вход			Далее создадим все возможные новые состояния, которые могут получиться в результате сочетаний исходных состояний, и занесём их в таблицу. Новые состояния будем записывать в виде {pq}. Тогда из состояния p по символу 1 переход будет происходить в такое состояние pq. В таблице присутствуют недостижимые состояния q, r, pr и qr, которые можно удалить без изменения результата.
состояние	0	1
p	{p}	{pq}
q	–	{r}
r	–	–
pq	{p}	{pqr}
pr	{p}	{pq}
qr	–	{r}
pqr	{p}	{pqr}

Можно было упростить процесс и сразу заносить в новую таблицу только те состояния, которые действительно могут возникнуть. Тогда состояния pr и qr в ней бы не появились. После удаления недостижимых состояний таблица примет вид:

	вход			Для удобства переобозначим состояния: заменим p на A, pq на B, pqr – на C. Тогда начальным состоянием будет A, конечным C.				вход
состояние	0	1	состояние			0		1
p	{p}	{pq}	A			{A}		{B}
pq	{p}	{pqr}	B			{A}		{C}
pqr	{p}	{pqr}	C			{A}		{C}

В итоге полученный детерминированный автомат, эквивалентный исходному НКА, будет иметь вид: M=({A,B,C},{0,1},,A,{C}), граф функции переходов :

Пусть q₁ и q₂ – состояния автомата M, на вход подается цепочка символов w длины k0: wV^*, wk, (q₁,w) ├─* (q₃,), (q₂,w) ├─* (q₄,). Если одно из состояний (q₃ или q₄) входит в F, а другое – нет, то говорят, что цепочка w различает состояния q₁ и q₂. Если же для любой входной цепочки w длины k она не различает состояния q₁ и q₂, то говорят, что они являются k-эквивалентными или k-неразличимыми. Множество K-эквивалентных состояний составляет класс эквивалентности R(k).

Очевидно, что множества F и Q\F являются 0-эквивалентными, записывается этот факт следующим образом: R(0)={F,Q\F}.

Для построения минимального автомата строятся классы эквивалентности R(n).

Алгоритм 3.3. Построение классов эквивалентности:

1. Полагаем n:=0, строится R(0)= {F,Q\F}.

2. n:=n+1. Строится R(n) на основании R(n–1): в класс эквивалентности R(n) входят те состояния, которые по одинаковым символам переходят в n–1-эквивалентные состояния: R(n):={r_ij(n): {q_ijQ: aV (q_ij,a) r_j(n–1)} i,jN}.

3. Если R(n)= R(n–1), то работа заканчивается. Иначе переход на шаг 2.

Алгоритм 3.4. Минимизация автомата:

1. Исключить все недостижимые состояния.

2. Построить классы эквивалентности.

3. Каждый из этих классов становится состоянием нового автомата.

4. Функция переходов строится на основании функции переходов исходного автомата и новых состояний.

Рассмотрим пример. Пусть ДКА имеет вид: M = ({q₀, q₁, q₂, q₃, q₄, q₅}, {0,1}, , q₀, {q₄, q₅}), а функция переходов задана графом:

Требуется минимизировать данный автомат.

Недостижимых состояний нет. Построим классы эквивалентности: R(0)={{q₀,q₁,q₂,q₃}, {q₄,q₅}}. Из состояния q₂ по 0 происходит переход в q₃, а из q₁ – в q₄. Состояния q₃ и q₄ находятся в разных классах эквивалентности R(0)  q₁ и q₂ будут входить в разные классы R(1). Аналогично рассуждая про остальные состояния, получим: R(1)={{q₄,q₅},{q₀,q₂},{q₁,q₃}}. Аналогично: R(2)={{q₄,q₅}, {q₀,q₂}, {q₁,q₃}}.  В новом автомате 3 состояния. Обозначим их по номеру одного из состояний каждого класса. M’ = {q₀,q₁,q₄}, {0,1}, ’, q₀, {q₄}).

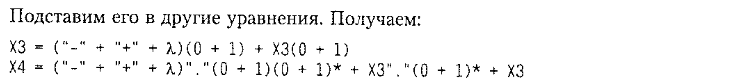
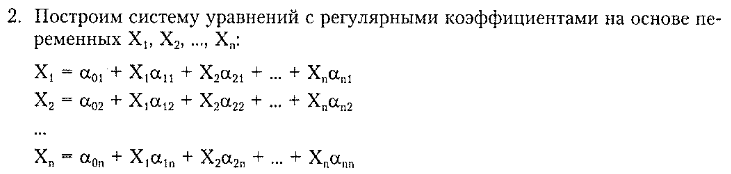
3.3.5 Расширения регулярных выражений

С тех пор как в 1950-х годах Клини (Kleene) ввел регулярные выражения с ба­зовыми операторами для объединения, конкатенации и замыкания Клини, к ним было добавлено много расширений, повышающих их способность определять строковые шаблоны. К сожалению, в настоящее время не определены стандарты на запись расширенных регулярных выражений, и в языках программирования нотация записи шаблонов может несколько отличаться. Здесь мы рассмотрим несколько расширений в записи ре­гулярных выражений, которые первоначально появились в утилитах Unix, таких как Lex, и которые в особенности полезны при определении лексических ана­лизаторов.

Выражение	Соответствие	Пример
с	Один неоператорный символ с	а
\с	Символ с буквально	\*
"s"	Строка s буквально	"**"
•	Любой символ, кроме символа новой строки \n	а.*b
^	Начало строки	^аbс
$	Конец строки	abc$
[s]	Любой символ из s	[abc]
[^s]	Любой символ, не входящий в s	[^abc]
r*	Нуль или более строк, соответствующих r	а*
г+	Одна или более строк, соответствующих r	а+
г?	Нуль или одно r	а?
r{m,n}	От т до n повторений r	а{1,5}
r1r2	r1, за которым следует r2, конкатенация	ab
r1|r2	r1 или r2, объединение	а|b
(г)	То же, что и r, группировка	(a|b)
r1/r2	r1, если за ним следует r2	abc/123

Рис. 3.8. Регулярные выражения Lex.

3.5 Генератор лексических анализаторов Lex

В этом разделе мы познакомимся с программным инструментом под названи­ем Lex (или, в более поздних реализациях, Flex), который позволяет определить лексический анализатор, указывая регулярные выражения для описания шабло­нов токенов. Входные обозначения для Lex обычно называют языком Lex, а сам инструмент — компилятором Lex. Компилятор Lex преобразует входные шаблоны в диаграмму переходов и генерирует код (в файле с именем lex.yy.c), ими­тирующий данную диаграмму переходов.

3.5.1 Использование Lex

На рис. 3.22 показана схема использования Lex. Входной файл lex.1 напи­сан на языке Lex и описывает генерируемый лексический анализатор. Компилятор Lex преобразует lex.1 в программу на языке программирования С в файле с име­нем lex.yy.c. Этот файл компилируется компилятором С в файл с названием а.out, как обычно. Выход компилятора С представляет собой работающий лекси­ческий анализатор, который может получать поток входных символов и выдавать поток токенов.

Рис. 3.22. Создание лексического анализатора с помощью Lex

Обычно скомпилированная программа на языке С, которая на рис. 3.22 по­казана как a.out, используется в качестве подпрограммы синтаксического ана­лизатора. Это функция на языке программирования С, которая возвращает целое число, представляющее собой код одного из возможных имен токенов. Значе­ние атрибута, которое может быть другим числовым кодом, указателем на запись таблицы символов или просто отсутствовать, помещается в глобальную перемен­ную yylval¹, которая совместно используется лексическим и синтаксическим анализаторами. Этот метод позволяет вернуть из функции как имя токена, так и значение его атрибута.