15. Лексический анализ, регулярные грамматики и конечные автоматы.

Разработка лексического анализатора – сканера, выполняется достаточно просто, если воспользоваться хорошо разработанным математическим аппаратом – теорией регулярных языков и конечных автоматов. В рамках этой теории классы однотипных лексем (идентификаторы, ключевые слова, константы и т.д.) рассматриваются как формальные языки – язык идентификаторов, констант, ключевых слов и т.д. Причём эти языки настолько просты, что они порождаются простейшей из грамматик – регулярной грамматикой.

Регулярная грамматика – это основа математической модели конечного автомата, который моделирует в свою очередь процесс лексического анализа текста исходной программы. Основной задачей лексического анализа является распознание лексических единиц. Существует различные типы конечных автоматов. Если результатом работы является лишь указание на то, что входная последовательность символов допустима или нет, то такой конечный автомат называется конечным распознавателем.

Конечный автомат строится следующим образом. Любая регулярная грамматика G(N,T,H,S) может быть представлена направленным графом, с помеченными узлами и дугами. Каждый узел помечаем символом из N, кроме конечного помечаемого символом #. Согласно принятым соглашениям, узел, соответствующий аксиоме языка S помечаем стрелкой ↓, а конечный узел изображаем в виде прямоугольника. Каждая дуга соответствует только одной продукции заданной грамматики G. Например, пусть регулярная грамматика G имеет следующие продукции:

S→aA|bB

A→aA|a

B→bB|d.

Тогда граф, отображающий данную грамматику G, будет иметь вид, представленный на рис.2. Путь на графе всегда соединяет начальную вершину с конечной вершиной графа. Метки, ассоциированные с дугами, составляющими этот путь, образуют некоторую строку. Множество таких строк совпадёт с языком Ɫ(G). Конкретные пути на графе будут соответствовать некоторой схеме вывода. Например,

S→aA→aaA→aaaA→aaaa

Этот путь от S к А, от А к А и от А к #. Конечный направленный граф, имеющий начальный узел и один или более конечных узлов сети – есть конечный автомат.

S

A

a a

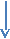
b a

B

#

b

b

Рис 15.1. Граф конечного автомата для заданной регулярной грамматики.

Можно дать и второе определение конечного автомата. Конечным автоматом (КА) называется совокупность пяти множеств:

КА={N,T,t,S,F}

где: N – конечное множество состояний автомата, совпадающее с

множеством нетерминальных символов грамматики;

T – множество терминальных символов автомата, совпадающее с

множеством терминальных символов грамматики;

t – функция переходов, задаваемая таблицей;

S – начальное состояние автомата, совпадающее с аксиомой грамматики;

F – конечные состояния автомата.

Функция переходов может быть представлена различными способами. Основные из них: списком команд КА, диаграммой состояний и матрицей переходов.

Команда КА представляет собой следующую запись:

(A_i, a_j) → A_k ,

которая представляет собой переход в автомате из вершины A_i в вершину A_k по дуге a_j. Дл КА необходимо составлять такой список команд, причём он должен обязательно содержать переходы в конечную вершину, для нормального завершения работы автомата.

Диаграмма состояний это по сути граф КА. И он содержит полную информацию о КА.

Матрица переходов может быть записана в двух видах. Во-первых, строки матрицы – это вершины КА (нетерминальные символы), столбцы матрицы – терминальные символы, приписываемые соответствующим дугам графа КА. Все три способа равнозначны.

КА могут быть детерминированными – ДКА и недетерминированными НДКА. В детерминированном автомате из каждой вершины выходят дуги, все отмеченные различными метками – терминальными символами. В НДКА имеется хотя бы одна вершина с одинаково отмеченными дугами. Для программирования ДКА гораздо проще. ДКА и НДКА задают, по сути, эквивалентные языки, но имеет место теорема, что ДКА может принять некоторый язык Ɫ, если этот язык принимает НДКА. Переход от НДКА к ДКА осуществляется тривиально, за счёт введения дополнительных фиктивных состояний (вершин). Если из одной вершины выходит две дуги, обозначенные одинаково (НДКА), то одну дугу обозначаем по другому, но замыкаем её на фиктивное состояние, из которого проводим ранее переобозначенную дугу к требуемому состоянию (ДКА).

Для практических целей необходимо, чтобы КА сам определял момент окончания входной цепочки символов с выдачей сообщения о правильности или неправильности входной цепочки символов. Для этих целей входная цепочка считается ограниченной справа концевым маркером ├. И в диаграмму состояний КА вводят интерпретированные состояния: допустить входную цепочку как лексему, отвергнуть входную цепочку как лексему, запомнить ошибку во входной цепочке.

В общем случае может быть предложен следующий порядок построения лексического анализатора (ЛА) или сканера.

1. Выделить во входном языке на основании задающей грамматики множество классов лексем.

2. Для каждого класса построить регулярную (автоматную) грамматику.

3. Для каждой регулярной грамматики построить КА.

4. Определить условия выхода из ЛА (переход его в начальное состояние) при достижении произвольной лексемы из каждого класса лексем.

5. Разбить символы входного языка на непересекающиеся множества.

6. Построить матрицу переходов ЛА.

7. Выбрать формат и код дескрипторов для лексем.

8. Запрограммировать ЛА.

16. S-грамматики и магазинные автоматы.

Главная задача теории формальных языков и грамматик состоит в построении алгоритмов формального синтеза основных блоков транслятора. Причём такого, который бы находил все 100% лексических, синтаксических и семантических ошибок. Это возможно сделать, введя в рассмотрение математическую модель процесса трансляции. Такой моделью является магазинный автомат (МА). Магазинный автомат имеет следующую структуру.

Входная лента Магазинная память

#

├

Рис.16.1. Структура магазинного автомата.

├ − маркер конца записи на ленте, # − маркер дна магазина.

Магазинный автомат один из способов описания алгоритма распознавания языка. Магазинный автомат это распознающее устройство. Формально магазинный автомат задаётся семёркой объектов

М={A,Q,Г, δ, q, z, F}

А- конечное множество входных символов – входной алфавит,

Q- конечное множество внутренних состояний – алфавит состояний,

Г – конечное множество магазинных символов,

q – начальное состояние автомата,

z – начальный символ в магазинной памяти,

F – множество заключительных состояний,

δ – отображения (QxAxГ) → (QxГ), где х означает декартово произведение

множеств.

За один такт работы автомата из магазина можно удалять не более одного символа. Каждый шаг работы автомата задаётся множеством правил перехода автомата из одного состояния в другие. Переходы определяются:

- состоянием автомата,

- верхним символом в магазине,

- текущим входным символом на ленте.

Множество правил перехода называется управляющим устройством. В зависимости от получаемой информации, управляющее устройство (УУ) реализует один такт работы автомата, который включает три операции:

1). Операции над магазином:

- записать символ

- считать верхний символ

- оставить магазин без изменений.

2). Операции над состояниями:

- перейти в состояние

- остаться в прежнем состоянии.

3). Операции над входом:

- перейти к следующему входному символу и сделать его текущим

(сдвиг)

- оставить данный входной символ текущим, т.е. держать его до

следующего шага (держать).

Обработку входной цепочки автомат начинает в некотором выделенном состоянии при определённом содержимом магазина. Затем автомат работает по командам УУ. При этом выполняется либо завершение обработки, либо переход в новое состояние. Если выполняется переход, то он даёт новый верхний символ магазина, новый текущий символ и автомат переходит в новое состояние и цикл работы повторяется.

Автомат называется распознавателем, если у него два выхода «ДОПУСТИТЬ» и «ОТВЕРГНУТЬ».

Рассмотрим промер автомата, распознающего слова языка Ɫ{0ⁿ 1ⁿ}, т.е. слова, состоящие из нулей, за которыми идёт столько же единиц.

В данном случае:

A={0,1,├}, Q={q1,q2}, Г={z,#}

q1 – начальное состояние,

# − начальное содержимое магазина.

УУ работает в соответствии с таблицами для состояний q1 и q2.

Состояние q1:

.

Магазин	Входная лента
	0	1	├
z	q1, запись z, сдвиг	q2, чтение, сдвиг	отвергнуть
#	q1, запись z, сдвиг	отвергнуть	отвергнуть

Состояние q2.

Магазин	Входная лента
	0	1	├
z	отвергнуть	q2, чтение, сдвиг	отвергнуть
#	отвергнуть	отвергнуть	допустить

Работа автомата при распознании конкретной цепочки описывается обычно в виде последовательности конфигураций автомата: слева изображается «магазин», в середине «состояние», справа необработанная часть входной цепочки.

Рассмотрим конфигурации автомата для цепочки 000111├

#	q1	000111├
#z	q1	00111├
#zz	q1	0111├
#zzz	q1	111├
#zz	q2	11├
#z	q2	1├
#	q2	├

ДОПУСТИТЬ