ААААА
 матрицасының
матрицасының
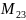 миноры
миноры
C) -5
E) теріс сан
F) бүтін сан
матрицасының
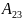 алгебралық толықтауышы
алгебралық толықтауышы
B) 5
D) оң сан
F) бүтін сан
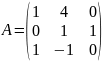 матрицасының
рангы
матрицасының
рангы
A) 3
E) 2-ден артық
G) 1-ден артық
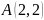 және
және
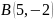 нүктелері берілген.
нүктелері берілген.
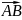 векторының абсциссасы
векторының абсциссасы
B) 3
E) бүтін сан
F) оң сан
және нүктелері берілген. векторының ординатасы
C) -4
E) бүтін сан
H) теріс сан
және нүктелері берілген. векторының ұзындығы
C) 5
E) бүтін сан
F) оң сан
және
нүктелері берілген.
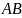 кесіндісінің ортасының
абсциссасы
кесіндісінің ортасының
абсциссасы
F) оң сан
G) 3,5
H) теріс сан
және нүктелері берілген. кесіндісінің ортасының
ординатасы
B) 0
E) бүтін сан
H) теріс емес сан
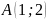 және
және
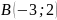 нүктелері арқылы өтетін түзудің теңдеуі
нүктелері арқылы өтетін түзудің теңдеуі
B)
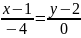
D)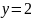
G)
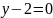
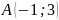 және
және
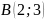 нүктелері арқылы өтетін түзудің теңдеуі
нүктелері арқылы өтетін түзудің теңдеуі
A)
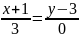
C)
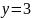
E)
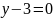
және
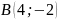 нүктелері арқылы өтетін түзудің теңдеуі
нүктелері арқылы өтетін түзудің теңдеуі
A)

C)
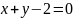
H)
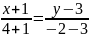
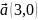 және
және
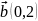 векторлардан құрылған параллелограммның
ауданы
векторлардан құрылған параллелограммның
ауданы
A) 6
E) бүтін сан
G) оң сан
Анықталмаған интегралдың қасиеттері
D)
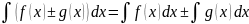
E)
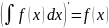
G)
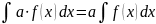
Айнымалыны ауыстыру тәсілімен табылатын интеграл
B)
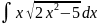
D)
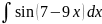
H)
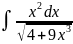
Анықталмаған коэффициенттер (жай бөлшектерге жіктеу) тәсілімен табылатын интеграл
D)
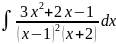
E)
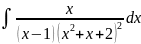
F)
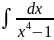
Айнымалылары ажыратылатын дифференциалдық теңдеу
A)
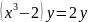
B)
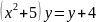
F)
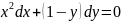
А(4,6) және В(–1,-4) нүктелері арқылы өтетін түзудің бұрыштық коэффициентін табу керек:
A) 2
C)
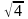
H)
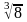
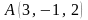 және
және
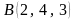 болса, онда
болса, онда
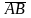 векторының координатасы тең: <variant>
векторының координатасы тең: <variant>
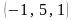
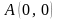 нүктесінен
нүктесінен
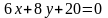 түзуіне дейінгі арақашықтық тең:<variant>
2
түзуіне дейінгі арақашықтық тең:<variant>
2
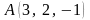 нүктесінен
нүктесінен
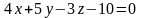 түзуіне дейінгі арақашықтық тең:
түзуіне дейінгі арақашықтық тең:
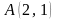 және
және
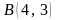 нүктелері
арқылы өтетін түзудің теңдеуі:<variant>
нүктелері
арқылы өтетін түзудің теңдеуі:<variant>
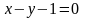
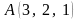 нүктесінен
өтетін және
нүктесінен
өтетін және
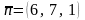 векторына
перпендикуляр болатын жазықтықтың
тедеуі:
векторына
перпендикуляр болатын жазықтықтың
тедеуі:
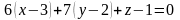
және
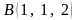 нүктелері
арқылы
өтетін түзудің канондық теңдеуі:
нүктелері
арқылы
өтетін түзудің канондық теңдеуі:
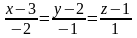
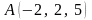 нүктесі
арқылы
нүктесі
арқылы
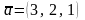 векторына
параллель өтетін түзудің канондық
теңдеуі:
векторына
параллель өтетін түзудің канондық
теңдеуі:
<variant>
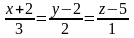
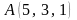 және
және
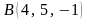 болса, онда
векторының координатасының ұзындығы
тең: <variant>
3
болса, онда
векторының координатасының ұзындығы
тең: <variant>
3
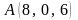 ,
,
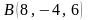 және
және
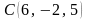
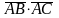 тең болады <variant>
8
тең болады <variant>
8
![]() және
және ![]() нүктелері берілген.
нүктелері берілген. ![]() векторының абсциссасы
векторының абсциссасы
$ 3 $ бүтін сан $ оң сан
және нүктелері берілген. векторының ординатасы
$ -4 $ бүтін сан $ теріс сан
және нүктелері берілген. векторының ұзындығы
$ 5 $ бүтін сан $ оң сан
және
нүктелері берілген. ![]() кесіндісінің ортасының абсциссасы
$ оң сан $ 3,5 $ теріс
сан
кесіндісінің ортасының абсциссасы
$ оң сан $ 3,5 $ теріс
сан
және нүктелері берілген. кесіндісінің ортасының
ординатасы $ 0 $ бүтін сан $ теріс емес сан
![]() және
және ![]() нүктелері арқылы өтетін түзудің теңдеуі
нүктелері арқылы өтетін түзудің теңдеуі
$
![]() $
$ ![]() $
$ ![]()
![]() және
және ![]() нүктелері арқылы өтетін түзудің теңдеуі
нүктелері арқылы өтетін түзудің теңдеуі
$
![]() $
$ ![]() $
$ ![]()
және ![]() нүктелері арқылы өтетін түзудің теңдеуі
нүктелері арқылы өтетін түзудің теңдеуі
$
![]() $
$ ![]() $
$ ![]()
Айнымалылары ажыратылатын дифференциалдық теңдеу
$
![]() $
$ ![]() $
$ ![]()
Анықталмаған интегралдың қасиеттері
$
![]()
$
![]()
$
![]()
Айнымалыны ауыстыру тәсілімен табылатын интеграл
$
![]() $
$ ![]() $
$ ![]()
Анықталмаған коэффициенттер (жай бөлшектерге жіктеу) тәсілімен табылатын интеграл
$
![]() $
$ ![]() $
$ ![]()
БББББ-ВВВВ
Баған-матрица
B)
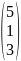
E)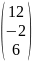
G)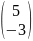
Біртекті теңдеулер жүйесі -
A)
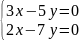
E)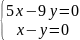
H)
Біртекті емес теңдеулер жүйесі -
B)
C)
D)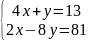
Бөліктеп интегралдау арқылы табылатын интеграл
A)
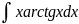
C)
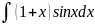
F)
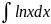
Бірінші ретті сызықтық дифференциалдық теңдеу
B)
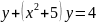
C)
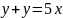
D)

Бірінші ретті дифференциалдық теңдеу
C)

E)
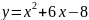
H)
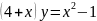
Берілгені:
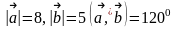 .
Табу керек:
.
Табу керек:
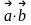 :
:
А) -20
C)-40/2
D)-60/3
Берілгені:
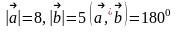 .Табу
керек:
.
.Табу
керек:
.
А) -40
E)-80/2
H)-120/3
Берілгені:
![]() табу
керек:
табу
керек:
![]()
A) 1
C) 2
E) 4/2
Берілгені:
![]() табу керек:
табу керек:
A) 12
C) 24/2
D) 36/3
Берілгені:
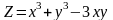 .
Табу керек:
.
Табу керек: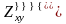 :
:
D) -3
E)
-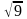
H) -6/2
Бөліктеп интегралдау арқылы табылатын интеграл
$
![]() $
$ ![]() $
$ ![]()
Бірінші ретті дифференциалдық теңдеу
$
![]() $
$ ![]() $
$ ![]()
Бірінші ретті сызықтық дифференциалдық теңдеу
$
![]() $
$ ![]() $
$ ![]()
Біртекті теңдеулер жүйесі -
$
![]() $
$ ![]() $
$![]()
Біртекті емес теңдеулер жүйесі -
$
![]() $
$ ![]() $
$ ![]()
Берілгені:
![]() .
.
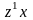 -тің
-тің
![]() нүктесіндегі мәнін табу керек:
нүктесіндегі мәнін табу керек:
C) 4
D)
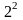
G)

Бұрыштық
коэффициенті
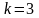 және
және
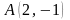 нүктесі
арқылы өтетін түзудің теңдеуі:
<variant>
нүктесі
арқылы өтетін түзудің теңдеуі:
<variant>
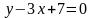
Бірінші
тамаша шек: <variant>

Векторлардың компланарлық шарты
A) аралас туынды нөлге тең
E) осы векторлардан құрылған параллелепипедтің көлемі нөлге тең
G) осы векторлардан құрылған пирамиданың көлемі нөлге тең
Векторлардың компланарлық шарты
$ аралас туынды нөлге тең
$ осы векторлардан құрылған параллелепипедтің көлемі нөлге тең
$ осы векторлардан құрылған пирамиданың көлемі нөлге тең
Гиперболаның
канондық теңдеуі:<variant>
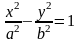
-ДДД
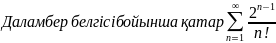
A) жинақты
C)
жинақты, өйткені
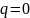
F)
жинақты, өйткені
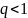
ЕЕЕЕ-
Екі вектордың векторлық көбейтіндісінің модулі
C) осы векторлардан құрылған параллелограммның ауданына тең
F) теріс емес сан
H) осы векторлардан құрылған үшбұрыштың екі еселенген ауданына тең
Екінші ретті дифференциалдық теңдеу
A)
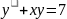
F)
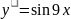
G)
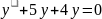
Екінші ретті сызықтық дифференциалдық теңдеудің сипаттаушы теңдеуінің түбірлері
C)
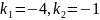
F) екі түбірі де теріс сан
G) екі түбірі де бүтін сан
Екі вектордың векторлық көбейтіндісінің модулі
$ осы векторлардан құрылған параллелограммның ауданына тең
$ теріс емес сан
$ осы векторлардан құрылған үшбұрыштың екі еселенген ауданына тең
Екі
нүкте арқылы өтетін түзудің
теңдеуі:<variant>
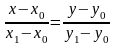
Екіншіі
тамаша шек:<variant>
ЖЖЖЖЖ
Жинақтылыққа Даламбер белгісімен зерттелетін қатардың жалпы мүшесі
C)
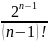
D)
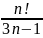
E)
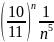
Жинақтылыққа Кошидің радикалдық белгісімен зерттелетін қатардың жалпы мүшесі
A)
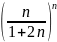
D)
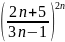
G)
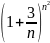
H)
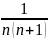
Жинақтылыққа Кошидің радикалдық белгісімен зерттелетін қатардың жалпы мүшесі
A)

C)
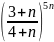
D)
Жинақтылыққа Лейбниц белгісімен зерттелетін қатардың жалпы мүшесі
B)
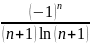
D)

F)
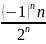
Жинақтылықтың қажетті белгісі орындалатын қатардың жалпы мүшесі
B)
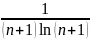
D)
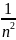
F)
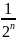
Жинақтылыққа салыстыру белгісімен зерттелетін қатардың жалпы мүшесі
B)
D)
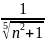
E)
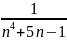
Жинақтылыққа Даламбер белгісімен зерттелетін қатардың жалпы мүшесі
A)
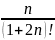
C)
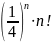
E)
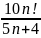
Жинақтылықтың қажетті белгісі орындалатын қатардың жалпы мүшесі
B)
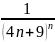
D)
E)
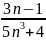
61 Жұп функция
B)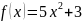
E)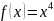
H)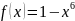
63 Жұп та емес, тақ та емес функция
A)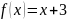
D)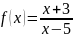
H)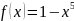
Жазықтықтың
жалпы теңдеуі:<variant>
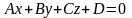
Жұп
функция
$![]() $
$![]() $
$![]()
Жұп та емес, тақ та емес функция
$![]() $
$![]() $
$![]()
Жинақтылыққа Даламбер белгісімен зерттелетін қатардың жалпы мүшесі
$
![]() $
$ ![]() $
$ ![]()
Жинақтылыққа Кошидің радикалдық белгісімен зерттелетін қатардың жалпы мүшесі
$
![]() $
$ ![]() $
$ ![]()
Жинақтылыққа Кошидің радикалдық белгісімен зерттелетін қатардың жалпы мүшесі
$
![]() $
$ ![]() $
$
Жинақтылыққа Лейбниц белгісімен зерттелетін қатардың жалпы мүшесі
$
![]() $
$ ![]() $
$ ![]()
Жинақтылықтың қажетті белгісі орындалатын қатардың жалпы мүшесі
$
![]() $
$ ![]() $
$ ![]()
Жинақтылыққа салыстыру белгісімен зерттелетін қатардың жалпы мүшесі
$
$ ![]() $
$ ![]()
Жинақтылыққа
Даламбер белгісімен зерттелетін
қатардың жалпы мүшесі
$ ![]() $
$ ![]() $
$ ![]()
Жинақтылықтың қажетті белгісі орындалатын қатардың жалпы мүшесі
$
![]() $
$
$
$ ![]()
ККК-ҚҚҚ
Квадрат матрица
A)
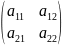
F)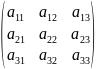
H)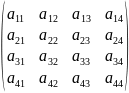
Қатар-матрица
A)
D)
H)
Кривая
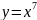
A)
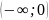 аралығында дөңес
аралығында дөңес
D)
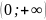 аралығында ойыс
аралығында ойыс
H)
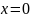 – иілу нүктесі
– иілу нүктесі
Квадрат үшмүшелікте толық квадратты ажырату тәсілімен табылатын интеграл
B)
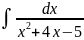
D)
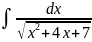
G)
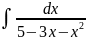
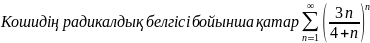
B) жинақсыз
G)
жинақсыз, өйткені
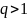
H)
жинақсыз, өйткені
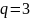
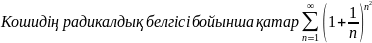
B) жинақсыз
E)
жинақсыз, өйткені
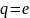
G) жинақсыз, өйткені
Квадрат
үшмүшелікте толық квадратты ажырату
тәсілімен табылатын интеграл
$ ![]() $
$ ![]() $
$ ![]()
Кошидi
радикалды белгici бойынша катар
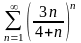
$
жинақсыз $ жинақсыз, өйткені ![]() $ жинақсыз, өйткені
$ жинақсыз, өйткені ![]()
Кошидi
радикалды белгici бойынша катар
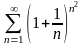
$
жинақсыз $ жинақсыз, өйткені ![]() $ жинақсыз, өйткені
$ жинақсыз, өйткені
Келесі
сызықтармен шектелген фигураның ауданын
табу керек:
![]()
A) 9
C) 18/2
E) 27/3
Келесі
сызықтармен шектелген фигураның ауданын
табу керек:
![]()
A) 8
B) 16/2
E) 24/3
Келесі
сызықтармен шектелген фигураның ауданын
табу керек:
![]()
A) 6
C) 12/2
H) 18/3
Келесі
сызықтармен шектелген фигураның ауданын
табу керек:
![]()
A) 35
B) 70/2
D) 105/3
Келесі
сызықтармен шектелген фигураның ауданын
табу керек:
![]()
D) 1
G) 2/2
H) 8/8
Келесі
сызықтармен шектелген фигураның ауданын
табу керек:
![]()
C) 2
E) 4/2
H) 6/3
Келесі
сызықтармен шектелген фигураның ауданын
табу керек:![]()
A) 48
E) 96/2
H) 144/3
Келесі
сызықтармен шектелген фигураның ауданын
есепте:
![]()
A) 64
E) 6,4 10
G) 0,64 102
Квадратная матрица
$
![]() $
$ 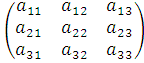 $
$ 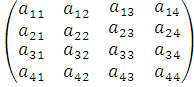
Қатар-матрица
$ ![]() $
$ ![]() $
$![]()
Қисық
![]() $
$ ![]() аралығында дөңес
аралығында дөңес
$
![]() аралығында ойыс $
аралығында ойыс $ ![]() – иілу нүктесі
– иілу нүктесі
ЛЛЛ
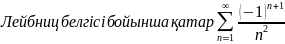
A) жинақты
C)
жинақты, өйткені
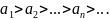
D)
жинақты, өйткені

Лейбниц
белгici бойынша катар
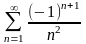
$
жинақты $ жинақты, өйткені ![]()
$
жинақты, өйткені ![]()
Мына өлшемді матрицалардың айырмасын табуға болады:
B)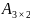 и
и
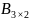
E)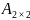 и
и
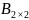
H)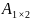 и
и

Мына өлшемді матрицалардың қосындысын табуға болады:
A)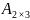 и
и
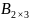
E)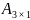 и
и
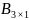
G)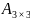 и
и
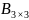
Мына өлшемді матрицалардың көбейтіндісін табуға болады:
B) и
C) и
G) и
Мына матрица үшін кері матрицаны табуға болады:
A)
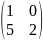
F)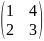
G)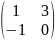
Матрицаның рангы мына жағдайларда өзгермейді:
A) кез-келген екі қатарын (бағанын) ауыстырғаннан
D)
кез-келген қатарының (бағанының)
элементтерін
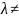 0
санына көбейткеннен
0
санына көбейткеннен
F) кез-келген қатардың элементтеріне 0 санына көбейтілген басқа қатардың элементтерін қосқаннан
М
(1;-2) нүктесінде
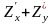 -нің
мәні, егер
-нің
мәні, егер
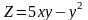
A) -1
C)
-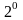
F)
-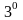
М1(-1; 2; 3), М2(3; -4; 2) екi нүктенiң арақашықтығын тап:
А)
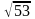
C)

E)
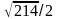
М1(3; 2; 1), М2(4; -3; 2) екi нүктенiң арақашықтығын тап:
А)
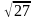
G)
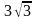
H)
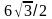
 екi
нүктенiң ара қашықтығын тап:
екi
нүктенiң ара қашықтығын тап:
A) 5
C) 10/2
H) 15/3
М1(1; 1; -3), М2(-4; 0; 3) екi нүктенiң арақашықтығын тап:
А)
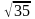
C)
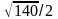
G)
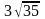
Мына матрица үшін кері матрицаны табуға болады:
$
![]() $
$![]() $
$![]()
Мына өлшемді матрицалардың айырмасын табуға болады:
$
![]() и
и ![]() $
$ ![]() и
и ![]() $
$ ![]() и
и ![]()
Мына өлшемді матрицалардың қосындысын табуға болады:
$
![]() и
и ![]() $
$ ![]() и
и ![]() $
$ ![]() и
и ![]()
Мына өлшемді матрицалардың көбейтіндісін табуға болады:
$ и $ и $ и
Матрицаның рангы мына жағдайларда өзгермейді:
$ кез-келген екі қатарын (бағанын) ауыстырғаннан
$
кез-келген қатарының (бағанының)
элементтерін ![]() 0
санына көбейткеннен
0
санына көбейткеннен
$ кез-келген қатардың элементтеріне 0 санына көбейтілген басқа қатардың элементтерін қосқаннан
ПП
Паробола
ушин
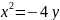
B)
төбесі
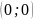 нүктеде
нүктеде
D)
директриса теңдеуі
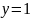
F)
фокусы