МИЭТ

Статическое моделирование парадокса дней рождения

Лабораторная работа по математическому моделированию

Выполнила: Кирпичёва Ольга, МП-34

01.01.2011

Статическое моделирование парадокса дней рождения

1. Постановка задачи

Описание

Парадокс дней рождения гласит, что в группе из 23 человек вероятность того, что у каких-либо двух человек дни рождения совпадут, превышает 50% (а именно, равна 50,7%). А для группы из 50 человек такая вероятность составит 97%, для 100 – 99,99996%. Такой результат на первый взгляд противоречит здравому смыслу, поэтому данный факт и был назван парадоксом.

Объект исследования

Исследование будет заключаться в рассмотрении изначально заявленного утверждения и схожих с ним задач, при смешении которых и происходит неверная оценка вероятности парадокса.

Моделируемые задачи:

1. Нахождение вероятности совпадения дней рождения у любыхдвухчленов группы.

2. Нахождение вероятности совпадения дней рождения у двухопределённыхчленов группы.

3. Нахождение вероятности совпадения дней рождения у какого-либочлена группы сопределённымчеловеком.

4. Нахождение вероятности совпадения дней рождения у любых mчленов группы.

5. Исследование случайной величины - числа опрошенных до первого совпадения дня рождения у любых двоих человек

Цель работы – подтверждение теоретических выкладок с помощью моделирования данных задач.

Моделирование будет производиться с помощью программного пакета MATLAB.

2. Решение задачи Упрощение модели

Для облегчения задачи моделирования будем считать, что дни рождения распределены равномерно, т.е. нет високосных лет, близнецов, рождаемость не зависит от времени года и других факторов.

Теоретическое решение задачи Задача 1.

Найдём вероятность следующего события: A(n) = {Есть хотя бы одно совпадение дней рождений в группе изnчеловек}. Противоположным ему событием будет = {Все дни рождения в группе изnчеловек различны}. Очевидно, что приn> 365и, следовательно,. Рассмотрим теперь задачу для .

Множество всех возможных исходов: .

Количество всевозможных вариантов расположения дней рождений в группе из nчеловек:.

Количество вариантов выбора дней рождения для события :

.

(‑ размещение без повторений изnпоk.)

Вероятность события :.

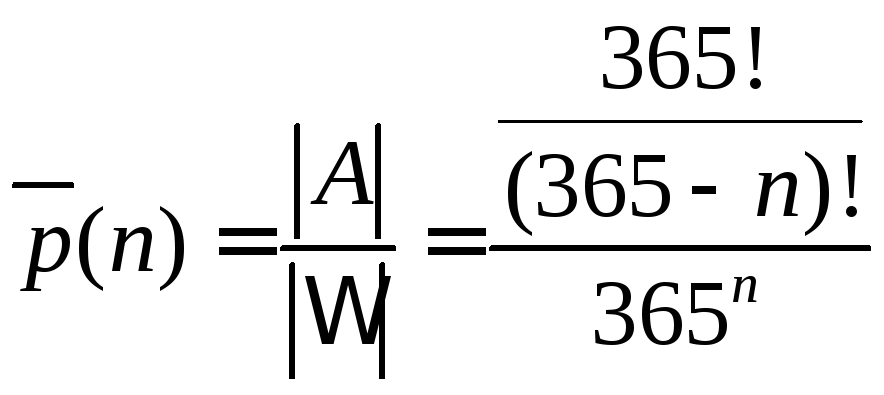Следовательно, вероятность события A(n) равна:

.

Таким образом, , что и требовалось доказать.

Составим небольшую таблицу значения вероятностей для некоторых n.

1. Вероятность p(n)

n	p(n)
5	0.0271
10	0.1170
20	0.4114
30	0.7063
50	0.9704
70	0.99916
100	0.9999997
367	1

Задача 2.

Вероятность события B={Совпадение дат дней рождения у двух определённых людей} рассчитывается другим образом.

Множество всех возможных исходов остаётся прежним: . (Выбираем две даты.) Вероятность выбора двух различных дат равна

.

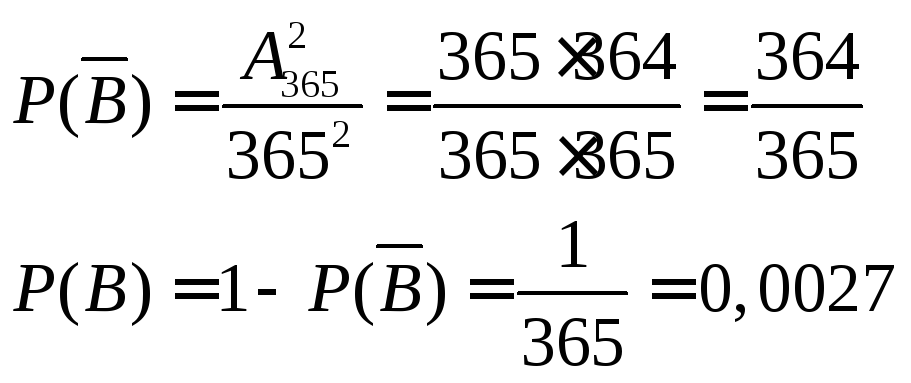Таким образом, вероятность совпадения дней рождения у двух конкретных людей крайне мала и не зависит от группы, в которой эти люди находятся.

Задача 3.

Рассмотрим событие С={Найдётся хотя бы один человек в группе из nчеловек, у которого день рождения совпадает с другим определённым человеком, не принадлежащим этой группе}.

. Опять же рассмотрим противоположное событие, т.е. ни у кого день рождения не совпадёт с заданным. Тогда для каждого члена группы есть 364 варианта дня рождения, и

.

Таким образом, вероятность события С будет равна

.

Для группы из 23 человек . Ещё несколько значений вероятности:.

Таким образом, стало понятно, что при незначительных на первый взгляд изменениях условия задачи полученная вероятность меняется кардинально.