2. Уравнения движения смеси газов

2.1. Уравнение неразрывности

Применительно к некоторой массе жидкости или газа, занимающего произвольно выделенный объем, закон сохранения массы можно сформулировать в следующем виде: масса жидкости или газа, состоящая из одних и тех же частиц, в процессе движения остается постоянной.

Естественно предполагается, что скорости движения жидких частиц значительно меньше скорости света, а это позволяет пренебречь релятивистскими эффектами изменения массы.

Движение жидких частиц будем рассматривать в трехмерном ортогональном пространстве с декартовыми координатами и единичными ортами . Слово «ортогональность» означает взаимную перпендикулярность координатных осей.

Используем часто применяемые в современной физической и математической литературе правила, позволяющие упростить запись: каждый буквенный индекс, встречающийся в выражении один раз, может принимать значения 1, 2, 3.

При этом, поскольку для обозначения координатных осей выбраны буквы с индексами ( ), под записью , например, будем понимать совокупность трех проекций скорости ; запись означает совокупность величин: .

По дважды повторяющемуся в одночлене индексу (за немногими, всегда оговариваемыми случаями) следует производить суммирование от 1 до 3.

Таким образом, выражения означают:

,

, (2.1.1)

.

Индексы суммирования часто называются «немыми» в том смысле, что сумма, очевидно, не меняет значение, если заменить «немой» индекс другой буквой: и т.д.

Во избежание путаницы в обозначениях индексы, относящиеся к химическому элементу или соединению, там, где это необходимо, будем для векторных и тензорных величин ставить вверху.

Так, например, выражение может обозначать проекцию скорости k-го химического компонента на ось .

Скалярные величины, такие как плотность, температура, давление и т.д., поскольку они инвариантны по отношению к любому преобразованию координат, для химических соединений или элементов обозначаем, как и ранее, индексом внизу. Например, – плотность i-го компонента смеси.

Приняв во внимание сделанные замечания, перейдем к математической записи закона сохранения массы для смеси газов.

Плотность смеси найдем по формуле

. (2.1.2)

Скорость жидкой частицы определим как среднемассовую скорость всех компонентов, составляющих смесь:

. (2.1.3)

Масса газа, заключенная в объеме W и ограниченная замкнутой поверхностью S, равна:

. (2.1.4)

Будем считать, что внутри выделенного объема нет источников и стоков, через которые газ мог бы подаваться в заданный объем или извлекаться из него. Тогда масса газа, находившегося внутри объема W в момент времени t, в последующие моменты времени, в соответствии с законом сохранения массы, останется неизменной. Конечно при этом нужно учитывать смещение граничной поверхности S из-за движения граничных жидких частиц.

Итак, в момент времени t масса газа внутри объема W равна:

. (2.1.5)

За промежуток времени подынтегральная функция и объем W, занятый выделенными жидкими частицами, получили приращения:

. (2.1.6)

Подставляя соотношения (2.1.6) в (2.1.4), получим

. (2.1.7)

Изменение объема , связанное с перемещением за время граничной поверхности, равно:

, (2.1.8)

где – проекция скорости граничных жидких частиц на внешнюю (направленную из объема) нормаль к поверхности S.

С учетом формулы (2.1.8) выражения для интегралов по объему запишутся в виде

(2.1.9)

Так как масса газа m не меняется с течением времени, то полная производная по времени равна нулю:

. (2.1.10)

По определению производной,

. (2.1.11)

Подставляя в (2.1.11) зависимости (2.1.7) и (2.1.9) и переходя к пределу при , получим интегральную форму записи закона сохранения массы:

. (2.1.12)

В частном случае установившегося движения, когда параметры газа в каждой фиксированной точке пространства не меняются с течением времени, интегральная форма уравнения неразрывности примет вид

; . (2.1.13)

Для получения уравнения неразрывности в дифференциальной форме следует выбрать объем в виде прямоугольника с ребрами, параллельными координатным осям, разделить соотношение (2.1.12) на этот объем и перейти к пределу, стягивая объем в точку:

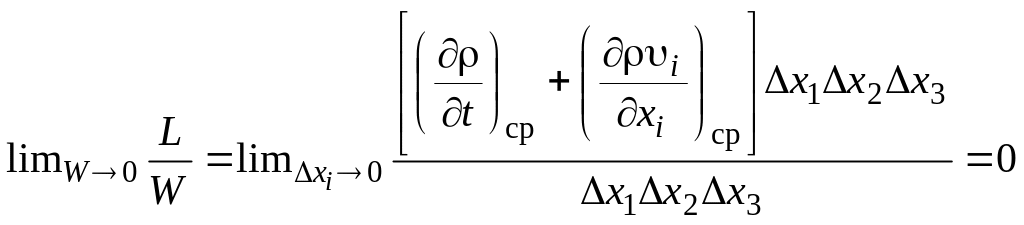, (2.1.14)

где и – средние по объему частные производные.

В результате получим уравнение неразрывности в дифференциальной форме в декартовой системе координат:

. (2.1.15)

Напомним, что по повторяющемуся индексу i в формуле (2.1.15) производится суммирование от 1 до 3.

Если второе слагаемое в (2.1.15) представить в виде

(2.1.16)

и учесть, что полная производная

, (2.1.17)

то (2.1.15) можно записать так:

. (2.1.18)

Для несжимаемой жидкости уравнение неразрывности примет вид

. (2.1.19)

В литературе зависимость вида (2.1.19) называется дивергенцией вектора:

. (2.1.20)

При использовании оператора Гамильтона, часто называемого также оператором набла :

, (2.1.21)

зависимость (2.1.19) можно записать в виде скалярного произведения:

. (2.1.22)

Заметим, что уравнение неразрывности для смеси газов записывается так же, как и для однокомпонентного газа, имеющего плотность и скорость, соответствующие смеси.