4.3. Определение параметров в начальном сечении изобарического участка сверхзвуковой нерасчетной струи

В соответствии с принятой моделью сверхзвуковой одиночной струи за начальное сечение изобарического участка и конец газодинамического взято сечение а–а, являющееся концом первой бочки. Если отдельные сверхзвуковые струи, входящие в блок, взаимодействуют на газодинамическом участке, то блочная струя заменяется эквивалентной по расходу и тяге одиночной струей. Таким образом, при расчете распределений газодинамических параметров в начальном сечении изобарического участка как одиночных, так и блочных струй достаточно найти параметры в одиночной эквивалентной струе.

Существуют два пути решения поставленной задачи. Первый путь – численное решение полной системы дифференциальных уравнений газовой динамики, описывающей течение турбулентного потока. Основное достоинство такого подхода – возможность определения требуемых значений газодинамических параметров в любой точке газодинамического участка, в том числе и в сечении а–а, недостаток – сложность и трудоемкость вычислений. Для упрощения вычислений часто пренебрегают трением в газе, что не позволяет учитывать развитие пограничных слоев на поверхностях тангенциальных разрывов. Это приводит к большим ошибкам при расчете распределений параметров в начальном сечении изобарического участка. Другой источник ошибок при использовании численных методов – это принимаемое допущение о неизменности термодинамических характеристик (показателей адиабаты, теплоемкостей, газовых постоянных и т.д.).

Второй путь основан на применении законов сохранения в интегральной форме, использовании некоторых экспериментальных результатов и априорно задаваемых профилей газодинамических параметров в начальном сечении изобарического участка. Назовем эти методы полуэмпирическими. Так как полуэмпирические методы опираются на опытные соотношения, они свободны от недостатков численных методов, но дают ограниченную информацию о распределении газодинамических параметров в области, занятой волновым участком струи. Заметим, что полуэмпирические методы позволяют учесть изменение термодинамических характеристик. В рамках поставленной задачи для определения параметров в начальном сечении изобарического участка удобнее использовать полуэмпирические методы, имея в виду, что их точность в сечении, проходящем через конец первой бочки, та же, что и численных (а в некоторых случаях даже выше), но вычислительный алгоритм проще.

Построим полуэмпирическую модель определения параметров в конце первой бочки, которая учитывает изменение термодинамических характеристик в процессе движения газа, а также перераспределение параметров в конце первой бочки из-за турбулентного смешения в зонах тангенциальных разрывов. Область, занятую струей в сечении а–а, разделим в общем случае на две подобласти: внутреннюю и внешнюю, в каждой из которых распределения газодинамических параметров пока принимаем однородными. Внутренняя подобласть, ограниченная пунктирными линиями на рис. 4.6, включает в себя часть потока, которая проходит через маховский диск. Естественно, что внутренняя подобласть вводится лишь тогда, когда есть маховский диск и его диаметр не слишком мал по сравнению с диаметром выходного сечения сопла d_вых (в практических расчетах внутреннюю подобласть следует вводить при d_мд / d_вых >0,15, где d_мд – диаметр маховского диска).

Определение параметров во внутренней подобласти. Параметры во внутренней подобласти вычисляются следующим образом. Предполагаем на основании имеющихся экспериментальных данных, что до значений чисел Маха на срезе сопла М_вых ≤ 4 поток за маховским диском ускоряется и в некотором сечении, называемом звуковым, скорость потока достигает скорости звука, а статическое давление сравнивается с величиной . Тогда, совмещая звуковое сечение с сечением а–а и принимая во внимание постоянство полного теплосодержания в пределах первой бочки при отсутствии перемешивания с окружающей средой:

, (4.3.1)

получим следующую замкнутую систему уравнений для определения газодинамических параметров во внутренней подобласти:

, ,

, ,

, ,

, , (4.3.2)

, ,

, ,

, ,

где индексом «вн» обозначены параметры во внутренней подобласти; , , – таблично заданные функции, найденные ранее при подготовке исходных данных, а – скорость звука, – давление, замеряемое трубкой Пито. Предполагается, что скорость в сечении а–а проецируется только на продольную ось, т.е. .

Система уравнений (4.3.2) решается методом последовательных приближений путем подбора величины , соответствующей значению , например методом половинного деления. Примем такую последовательность действий: устанавливаем первоначальный интервал возможных значений теплосодержаний во внутренней подобласти , делим этот интервал пополам и полученное в первом приближении значение используем для последовательного решения уравнений системы (4.3.2) и вычисления в первом приближении значений , , , и т.д. Если полученное в первом приближении значение , то верхняя граница интервала возможных величин переносится в точку , в противоположном случае нижняя граница этого интервала переносится в точку . Далее процесс деления интервала возможных значений повторяется до тех пор, пока не будет достигнута заданная точность определения газодинамических параметров во внутренней подобласти. Отметим, что в действительности звуковое сечение не совпадает с принятым в нашей модели сверхзвуковой струи положением начального сечения изобарического участка, а находится за этим сечением вниз по потоку, но вызываемая этим обстоятельством ошибка в определении газодинамических параметров на изобарическом участке струи незначительна.

Определение размеров внутренней подобласти. Определим диаметр внутренней подобласти , равный, пo предположению, диаметру звукового сечения. Так как внутренняя подобласть формируется потоком, прошедшим через маховский диск, то сначала следует найти размеры маховского диска. Для нахождения его диаметра в первой бочке сверхзвуковой нерасчетной струи, истекающей в затопленное пространство, воспользуемся приближенными экспериментальными соотношениями:

(4.3.3)

, ,

, (4.3.4)

, , ,

где – угол полураствора сопла. Соотношение (4.3.4) справедливо также для течений с отрывом в сопле, если вместо параметров на срезе взять параметры в сечении отрыва. Формула (4.3.4) получена при аппроксимации экспериментальных данных для струй, истекающих из конических сопл. При определении в перерасширенных струях, истекающих из профилированных сопл, рекомендуется зависимость

, (4.3.5)

, .

Однако в пределах точности рассматриваемой расчетной модели и обработки экспериментальных данных зависимость (4.3.4) может быть использована для встречающихся на практике углов при расчете струй, истекающих как из конических, так и из профилированных сопл.

Рассмотрим влияние числа Маха спутного потока на размеры маховского диска. Если величина , значения находятся по соотношениям (4.3.3), (4.3.4). Дальнейшее повышение приводит в недорасширенных струях к уменьшению значений , и если , , то можно принять равным нулю. Для промежуточных значений , величину будем определять приближенно, считая, что в указанном диапазоне значений меняется линейно от величины, даваемой формулой (4.3.3), которой ставится в соответствие значение , до нуля при . При в перерасширенных струях следует учитывать фактическое увеличение нерасчетности n и приближение ее к единице из-за разрежения, возникающего при обтекании сужающейся части струи. В результате этого процесс выравнивания статического давления по длине струи затягивается. Приближенно статическое давление во внешнем потоке у границы струи на участке сужения можно оценить по формуле Прандтля–Майера и тем самым учесть влияние спутного потока на перераспределение параметров в первой бочке. Но, принимая во внимание, что в прикладных задачах комбинация малых нерасчетностей с большими значениями встречается достаточно редко, ограничимся в разрабатываемом алгоритме использованием формулы (4.3.4) при всех значениях .

Таким образом, соотношения (4.3.3), (4.3.4) и сформулированные выше рекомендации дают возможность приближенно найти значения в диапазоне изменения параметров на срезе сопла и в окружающей среде, с которыми приходится сталкиваться на практике. В заключение отметим две особенности зависимостей (4.3.3), (4.3.4): получение отрицательных значений при некоторых сочетаниях значений и n, что трактуется как равенство нулю, и отсутствие в указанных формулах показателя адиабаты ввиду его незначительного влияния на .

Диаметр звукового сечения, равный, по предположению, диаметру внутренней подобласти , связан с величиной условием постоянства расхода в трубке тока, проходящей через маховский диск:

, (4.3.6)

где и – площади маховского диска и звукового сечения, – число Маха непосредственно за центральным скачком уплотнения, которое в свою очередь связано с числом Маха перед центральным скачком уплотнения и с коэффициентом потерь полного напора соотношениями

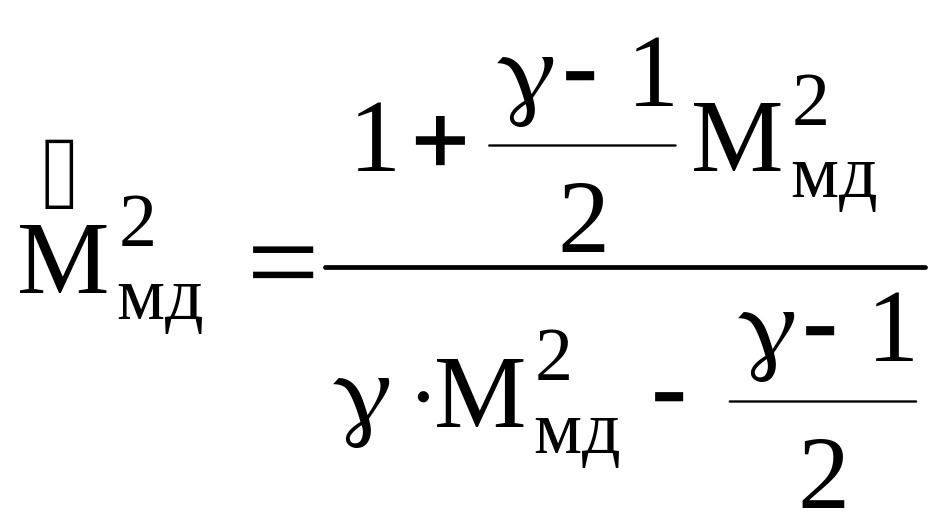, (4.3.7)

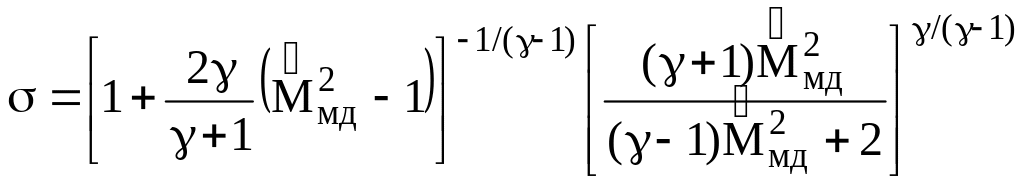, (4.3.8)

где , – давление адиабатически заторможенного потока перед маховским диском, определяемое по известным параметрам на срезе сопла:

, (4.3.9)

– давление адиабатически заторможенного потока за маховским диском, совпадающее с , так как течение газа от маховского диска и до звукового сечения во внутренней подобласти дозвуковое. Считая течение за маховским диском изоэнтропическим и учитывая, что в сечении а–а во внутренней подобласти , а , получим формулу для нахождения давления заторможенного потока:

. (4.3.10)

Показатель адиабаты в (4.3.6) – (4.3.10) принимается равным показателю адиабаты во внутренней подобласти , полученному ранее при решении (4.3.2). Алгоритм решения системы (4.3.6) – (4.3.10): по формулам (4.3.9) и (4.3.10) находят и ; определяют коэффициент потерь полного напора ; методом половинного деления при подборе числа Маха за центральным скачком уплотнения в возможном диапазоне его изменения решают уравнения (4.3.7), (4.3.8), неявным образом определяющие и ; по формуле (4.3.6) вычисляют диаметр и площадь внутренней подобласти.

Итак, приведенные уравнения и алгоритмы их решения позволяют определить размеры не только внутренней подобласти в начальном сечении изобарического участка, но и маховского диска, а также параметры потока до и после него.

Определение параметров во внешней подобласти и размеров струи в начальном сечении изобарического участка. Запишем систему уравнений, определяющую газодинамические параметры и размеры наружной подобласти в конце первой бочки. В соответствии с законами сохранения массы и количества движения

, (4.3.11)

(4.3.12)

где индексом «н» обозначаются параметры в наружной подобласти. Как и для внутренней подобласти, предполагается, что продольная составляющая скорости в наружной подобласти равна значению самой скорости .

Дополняя систему (4.3.11), (4.3.12) условием постоянства полного теплосодержания:

, (4.3.13)

предположением о равенстве статического давления в конце первой бочки давлению :

(4.3.14)

и таблично заданными функциями

, , , (4.3.15)

получим замкнутую систему для нахождения во внешней подобласти плотности , скорости , теплосодержания , температуры , газовой постоянной , показателя адиабаты, а также площади наружной подобласти .

Схема решения системы (4.3.11)–(4.3.15) проста: разделив (4.3.12) на (4.3.11), находим скорость ; подставив ее значение в (4.3.13), получим теплосодержание ; далее из (4.3.15) находим последовательно значения , и ; затем из (4.3.14) определяем плотность и, наконец, из (4.3.11) – площадь .

Теперь газодинамические комплексы , скорость звука , число Маха и некоторые вспомогательные комбинации газодинамических параметров во внешней зоне струи в сечении а–а, диаметр струи в этом сечении , среднемассовое по начальному сечению изобарического участка струи число Маха :

(4.3.16)

и параметр , характеризующий отношение средних плотностей в окружающей среде и сечении а–а,

, (4.3.17)

выражаются через известные величины:

, ,

, , ,

, , , (4.3.18)

, ,

.

О точности определения геометрических размеров струи, а следовательно, косвенно и о точности определения средних значений газодинамических параметров в конце первой бочки, можно судить, сравнивая приведенные в табл. 4.1 данные расчета по изложенной методике с результатами обработки теневых фотографий затопленных воздушных одиночных сверхзвуковых струй и – для некоторых режимов – эпюр . При обработке эпюр за идеальную границу струи принималась условно линия, на которой скоростной напор составлял . При обработке теневых фотографий устанавливалась точка в конце первой бочки, где начиналось резкое изменение кривизны отраженного скачка, что свидетельствовало о переходе к зоне значительных градиентов скорости. Эта точка считалась лежащей на внутренней границе наружного пограничного слоя. Точка пересечения условной идеальной границы струи с сечением а–а приближенно находилась как средняя между точками на внутренней и наружной границах внешнего пограничного слоя.

Т а б л и ц а 4.1