3. Методы расчета турбулентных струй

3.1. Интегральные методы расчета

Сложный характер турбулентного движения, которое пока не удается описать единой системой дифференциальных уравнений, обусловил широкое использование интегральных методов. Отличительной особенностью этих методов является задание в какой-либо форме профилей газодинамических параметров или их комбинаций. Это позволяет исключить из рассмотрения дифференциальные уравнения движения, энергии и диффузии и ограничиться использованием интегральных соотношений.

Проиллюстрируем применение метода интегральных соотношений к расчету основного участка струи, истекающей в затопленное пространство. На этом участке линейные размеры сопла пренебрежимо малы по сравнению с расстоянием от него, что позволяет считать течение автомодельным и принять срез сопла за точечный источник массы, количества движения и энергии.

Запишем выведенные ранее (см. формулы (2.2.9) – (2.2.13), (2.4.11), (2.5.9)) интегральные законы сохранения количества движения, энергии и массы для изобарических участков сжимаемых неизотермических струй или струй с диффузионным факелом горения:

, (3.1.1)

где , , , , – площадь струи в произвольном поперечном сечении на изобарическом участке, – площадь начального сечения изобарического участка.

Для струй, истекающих в затопленное пространство, , суммарное количество движения в сечении равно реактивной силе (см. формулу (2.2.12))

. (3.1.2)

На основе опыта установлено, что для турбулентной струи на достаточно больших удалениях от среза сопла характер изменения математических ожиданий комплексов по сечению струи на основном участке хорошо описывается экспоненциальными зависимостями вида

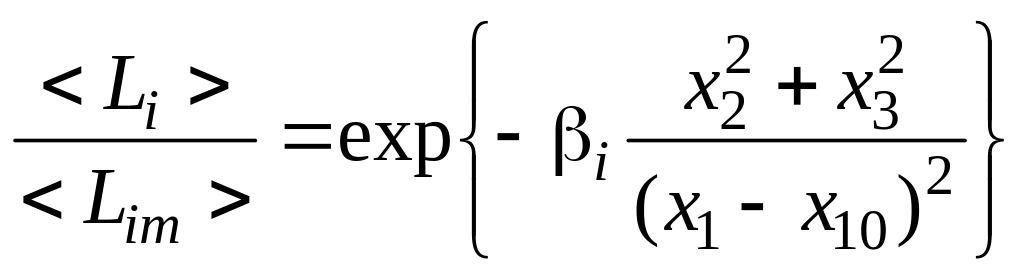, (3.1.3)

где индексом «m» обозначены параметры на оси; начало координат совмещено с центром выходного сечения сопла; – продольная координата, совпадающая с осью струи и отсчитываемая от среза сопла; – опытная константа, определяющая полюс струи; – опытные константы.

Дополним (3.1.1) – (3.1.3) уравнением состояния, которое для изобарического участка струи имеет вид

, (3.1.4)

и термодинамическими зависимостями, определяющими – для струй с физико-химическими превращениями, – для неизотермических струй без физико-химических превращений. Если теперь выразить математические ожидания комбинаций газодинамических параметров через математические ожидания этих параметров, то система (3.1.1) – (3.1.4) становится замкнутой и, решая её, находим искомые средние значения газодинамических параметров в требуемых точках основного участка струи.

В работах, в которых используются интегральные методы расчета струйных течений, явно или неявно предполагается, что математические ожидания произведений газодинамических параметров равны произведениям математических ожиданий. Обычно это предположение не приводит к значительным ошибкам при определении математических ожиданий газодинамических параметров. Однако возможны реальные ситуации, в которых указанное предположение делать нельзя. Например, при истечении водородной струи в воздух диффузионный факел располагается вблизи наружной границы струи и температура в факеле вследствие пульсаций газодинамических параметров снижается почти на 1000 К.

Аналогичным образом определяются газодинамические параметры в зонах смешения на начальном участке турбулентной струи. Автомодельными зонами струи в этом случае являются пограничные слои, развивающиеся на поверхностях тангенциальных разрывов скорости. Профили в сечениях пограничного слоя задаются зависимостями, полученными на основании обработки опытных данных.

При расчете блочных струй используется согласующийся с интегральными законами сохранения (3.1.1) и подтвержденный экспериментальными исследованиями принцип суперпозиции решений для комплексов :

, (3.1.5)

где – значение комплекса в заданной точке при работе всех двигателей, входящих в блок, – при работе лишь j-го двигателя блока.

Отметим, что, разбивая начальное сечение изобарического участка турбулентной струи на элементарные струйки, используя соотношения типа (3.1.1) для основного участка j-й струйки и выполняя суммирование комплексов в соответствии с формулой (3.1.5), можно найти распределение по всему полю, в том числе и на неавтомодельных участках, при произвольном законе распределения в начальном сечении.

Метод интегральных соотношений, базирующийся на зависимостях вида (3.1.1), может быть распространен с соответствующими видоизменениями, связанными с наличием продольного градиента давления, на струи в сносящем потоке.

Возможны и другие формы зависимостей, определяющих профили газодинамических параметров по сечению струи. Так, например, в работах Г.И. Абрамовича задаются профи- ли , , . В работах А.С. Гиневского

постулируется полиномиальный закон изменения турбулентного трения по сечению струи, что, с использованием гипотезы Прандтля о связи турбулентного трения с поперечным градиентом осредненной скорости, при соответствующих граничных условиях определяет, в конечном счете, профиль средней скорости. Известен еще ряд способов задания как аппроксимирующих зависимостей, так и комбинаций газодинамических параметров, для которых эти зависимости определены.

Вычисление среднеквадратических значений пульсаций газодинамических параметров и прочих вероятностных характеристик требует введения самостоятельных гипотез.

Среднеквадратическое значение пульсации некоторой величины обычно находится с помощью предположения о пропорциональности поперечному градиенту математического ожидания . Коэффициент пропорциональности, в общем случае зависящий от координат выбранной точки и параметров на срезе сопла и окружающей среды, определяется по соотношениям, обобщающим экспериментальные результаты. В практике расчетов турбулентных струй широко используется, например, выражение для на базе полуэмпирической теории Прандтля:

; , (3.1.6)

где – опытная константа, – путь смешения.

Следует заметить, что для струй с диффузионными факелом предположение о пропорциональности слишком грубо и приводит к большим количественным, а в ряде случаев и качественным ошибкам в определении среднеквадратических величин пульсаций в значительных областях. Так, в зоне диффузионного факела горения поперечные градиенты математических ожиданий плотности и температуры равны нулю, в то время как среднеквадратические значения пульсаций плотности и температуры в этих областях близки к максимальным. Аналогичная картина наблюдается, в частности, и на основном участке струи: пульсации газодинамических параметров на оси достаточно велики, в то время как соответствующие градиенты математических ожиданий в силу симметрии равны нулю.

В зоне смешения блочных струй по сечению может наблюдаться еще больше (пять и более) зон с нулевыми градиентами и и значительными величинами и .

Все это существенно ограничивает возможности применения соотношений типа (3.1.6) для определения среднеквадратических значений пульсаций газодинамических параметров в струях с диффузионным факелом.

Известны попытки "исправить" соотношения (3.1.6) введением слагаемых, пропорциональных второй производной от , что позволяет получить ненулевые значения при нулевых градиентах величины . Однако формулы подобного типа не получили широкого распространения из-за сложности расчетных соотношений и необходимости введения еще ряда эмпирических констант. К тому же эти формулы недостаточно универсальны.

В заключение обратим внимание на сильные и слабые стороны интегральных методов, имея в виду их использование при создании пакета прикладных программ.

Интегральные методы позволяют с достаточной для технических приложений точностью получить математические ожидания газодинамических параметров или их комбинаций без учета пульсационного движения. В большинстве случаев учет пульсаций не приводит к заметному обратному влиянию на искомые величины. Поэтому задачи определения характеристик осредненного и пульсационного движения могут решаться раздельно.

Основной недостаток метода интегральных соотношений - большие ошибки при определении характеристик пульсационного движения, часть из которых, например характерные масштабы пульсационного движения, в рамках интегральных методов вообще не определяются.

Наибольшей универсальностью обладает метод расчёта, основанный на использовании соотношений (3.1.1) – (3.1.5). По ним рассчитываются математические ожидания газодинамических параметров на автомодельных и неавтомодельных изобарических участках различных типов струй, включая блочные струи. Другие интегральные методы, рассмотренные ранее, например методы, основанные на задании профилей скорости и температуры, заметно меньше распространены: они используются лишь для определения газодинамических параметров на автомодельных участках одиночных струй.

Опытные константы, входящие в расчетные зависимости интегральных методов, зависят от числа Маха на срезе сопла, нерасчетности, отношения плотностей на срезе сопла и в окружающей среде, числа Маха спутного потока и т.д. Интересно отметить, что количество опытных констант и набор факторов, влияющих на их величину, примерно одинаковы не только для интегральных методов, но и для рассматриваемых далее полуэмпирических моделей расчета турбулентных струй.

Основное положительное свойство интегральных методов - возможность определения газодинамических и электрофизических параметров только в требуемых точках струй и по достаточно простым зависимостям даже для трехмерных струй. В результате избыточная информация в процессе счета исключается, а время на проведение расчетов существенно сокращается.