
- •Лекция №9
- •§2. Кривые второго порядка. Окружность
- •§3 10 . Эллипс
- •I. Определение эллипса. Вывод канонического уравнения.
- •II. График эллипса
- •III. Эксцентриситет эллипса
- •§ 14 4 10 . Гипербола
- •I. Определение. Каноническое уравнение.
- •II. График гиперболы
- •Симметрия
- •Вершины. Действительные и мнимые оси
- •А симптоты гиперболы
- •III. Равносторонняя гипербола
- •IV. Эксцентриситет гиперболы
- •§ 14 5 10 . Парабола
- •I. Определение параболы. Вывод канонического уравнения
- •II. Исследование формы параболы
- •I I. Различные виды парабол
- •§6. Преобразование координат
- •Параллельный перенос
- •II. Поворот осей координат
- •III. Общий случай преобразования координат
- •IV. Уравнение равносторонней гиперболы относительно асимптот
II. Поворот осей координат
На плоскости задана прямоугольная система координат Oxy. Повернем координатные оси на угол α, не меняя начала координат. Получим новую систему координат OХУ.
М – произвольная точка плоскости,
М (x;
y)
– в старой системе
(x;
y)
– в старой системе
координат Оху,
M(X;Y) – в новой системе
координат OXY.

Тогда (3) –
(3) –

формулы поворота координатных осей.
III. Общий случай преобразования координат
Пусть на плоскости заданы две декартовы прямоугольные системы координат Oxy и O1XY с разным началом и разными направлениями осей.

О1(а,b) координаты О1 в системе координат Oxy,
α – угол, который образует ось O1Xc осью Ox.
Возьмем т. М. М(x;y) – в координатной плоскости Oxy,
M(X;Y) – в координатной плоскости O1ХУ.
Введем
промежуточную систему координат O1 ,
где O1
,
где O1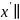 Ox,
O1
Ox,
O1 Oy.
Oy.
Переход от Oxy к O1XY осуществляется за два шага:


 α
+ b
α
+ b
Тогда
IV. Уравнение равносторонней гиперболы относительно асимптот
 –уравнение
равносторонней гиперболы.
–уравнение
равносторонней гиперболы.
y = х, у = – х – уравнения асимптот.
Повернем
координатные оси на угол
 .
Получим новую систему координат ОХУ,
где новыми осями координат являются
асимптоты.
.
Получим новую систему координат ОХУ,
где новыми осями координат являются
асимптоты.
По формулам (3) получим:
 ,
,

 ,
,

 ,
,

Подставим х и у в уравнение равносторонней гиперболы:
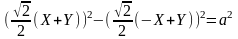
 ;
;
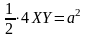 ,
,
 – уравнение
равносторонней гиперболы, когда осями
координат являются асимптоты.
– уравнение
равносторонней гиперболы, когда осями
координат являются асимптоты.
И зобразим
Оху
в обычном положении
зобразим
Оху
в обычном положении
XУ = k, k > 0
Е сли
повернуть оси Ох
и Оу
на угол
сли
повернуть оси Ох
и Оу
на угол
 ,
то получим
,
то получим
 .
XУ
=
k,
k
< 0.
.
XУ
=
k,
k
< 0.
