III. Равносторонняя гипербола

Если а = b, то гипербола называется равносторонней.

Из (3) – уравнение равносторонней гиперболы.

y = х, у = – х – уравнения асимптот равносторонней гиперболы (биссектрисы координатных углов).

IV. Эксцентриситет гиперболы

def. Эксцентриситетом гиперболы называется отношение расстояния между фокусами к длине действительной оси . т.к. с>а, то . Разделим на : , 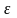характеризует степень сжатости гиперболы: чем меньше , тем более вытянут характеризующий прямоугольник вдоль оси Ох.

Пример 4.1. Составить уравнение гиперболы, длина действительной оси равно 16, эксцентриситет равен . Найти уравнения асимптот. Построить график.

§ 14 5 10 . Парабола

I. Определение параболы. Вывод канонического уравнения

def. Параболой называется геометрическое место точек, равноудаленных от данной точки, называемой фокусом, и от данной прямой, называемой директрисой.

О бозначим p – расстояние от фокуса до директрисы; р – параметр параболы.

F – фокус;

l – директриса;

M – произвольная точка параболы;

p – параметр параболы (расстояние от F до l).

– по определению параболы.

Выберем систему координат следующим образом: ось OX проведем через фокус F перпендикулярно директрисе l. Начало координат О поместим на равных расстояниях от F и l.

M (x; y) – производная точка параболы; F( ) – фокус

N( )  основание перпендикуляра, x = – уравнение директрисы

|MF|= , |MN|= .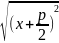

Из определения следует: = – уравнение параболы в выбранной системе координат.

Преобразуем это уравнение:

1.  каноническое уравнение параболы.

II. Исследование формы параболы

1. Из (1) получим: (1) расположена справа от оси OY (в правой полуплоскости)

2. + , любому х соответствуют два значения у + – , значит (1) симметрична относительно оси Оx.

3. Точка пересечение с Ох (с осью симметрии): у = 0 х = 0.

О (0;0)  вершина параболы.

4. Если х  +∞, то |y|  +∞.

I I. Различные виды парабол

1. y²= 2px – симметрична относительно Оx,

ветви вправо (в правой полуплоскости),

О (0;0)  вершина.

2. y²= –2px – симметрична относительно Ох,

ветви влево

(в левой полуплоскости),

О(0;0)  вершина.

3. х²=2pу – симметрична относительно Оу,

ветви вверх (в верхней полуплоскости),

О(0;0)  вершина.

4. х²= –2pу – симметрична относительно Оу,

ветви вниз (в нижней полуплоскости),

О (0;0)  вершина.

§6. Преобразование координат

1. Параллельный перенос

На плоскости введена прямоугольная система координат Oxy. Перенесем точку O в точку 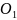и построим новую систему координат , причем , направления осей совпадают, единицы масштаба одинаковые.

Говорят, что выполнен параллельный перенос осей координат,

причем точка имеет координаты (a,b) в системе Oxy.

M – произвольная точка плоскости.

M(x, y) – в старой системе координат Oxy.

M(X, Y) – в новой системе координат .

(a, b) – координаты точки в старой системе координат.

Справедливы формулы:

X = x  a Y = y  b

x = X + a y = Y + b

 формулы, выражающие новые координаты через старые.

 формулы, выражающие старые координаты через новые.

Эти формулы называются формулами параллельного переноса.

З

амечание 1. Уравнения вида

(1) (2)

(2)

определяют параболу с вершиной в точке (a, b).

Действительно, с помощью формул параллельного переноса:

получим: (1)  ,

(2)  –

параболы с вершиной в новом начале координат .

Осью симметрии параболы (1) является прямая .

Осью симметрии параболы (2) является прямая .

Пример 6.1. Найти координаты вершины параболы, построить график:

а) ; б) .

Замечание 2. Если в уравнениях эллипса и гиперболы заменить х и у соответственно на и , то полученные уравнения будут определять те же линии, но со смещенным центром (вместо будет ). 