Лекция №9

§2. Кривые второго порядка. Окружность

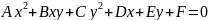(1) – общее уравнение второй степени относительно x и y, где A, B, C, D, E, F  R и A, B, C одновременно не равны 0. def. Кривой второго порядка называется линия, определяемая уравнением второй степени относительно текущих декартовых координат. Кривыми второго порядка являются: эллипс (частный случай – окружность); гипербола; парабола.

def. Окружностью называется геометрическое место точек плоскости, равноудаленных от данной точки, называемой центром.

Рассмотрим на плоскости Oxy (в прямоугольной декартовой системе координат) окружность радиуса R с центром в т. C (a; b) и составим её уравнение.

C (a; b) – центр окружности,

M(x; y) – произвольная точка окружности,

.

По определению  .

(2) – уравнение окружности с центром в т. C (a; b) и

радиусом R.

Частный случай:

– уравнение окружности с центром в т. O (0; 0) и радиусом R.

Раскроем скобки в уравнении (2): 

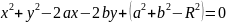. Обозначим ; ; .

– уравнение второй степени относительно x и y. Его особенности: .

Обратно, если в (1) , то (1) определяет окружность.

Пример 2.1. Дано уравнение 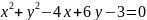. Доказать, что это уравнение определяет окружность. Найти центр и радиус.

§3 10 . Эллипс

I. Определение эллипса. Вывод канонического уравнения.

def. Эллипсом называется геометрическое место точек, сумма расстояния которых

до двух данных точек, называемых фокусами, есть величина постоянная.

Обозначим – фокусы,

M

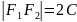– расстояние между фокусами.

М – производная точка эллипса.

2а – постоянная величина, равная сумме расстояний от М до .

= const = 2a (1) 

по определению эллипса.

2a > 2c  a >c.

Введем систему координат следующим образом: ось OX проведем через фокусы , начало координат поместим в середину отрезка 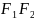. Ось OY проведем через середину отрезка перпендикулярно OX.

М (x; y) – произвольная точка эллипса,

(c; 0), 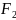(– c; 0) – фокусы эллипса.

0

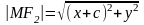, . Подставляя в (1), получим:

(2) – уравнение эллипса в выбранной системе координат.

Упростим данное уравнение: .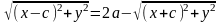

Возведем обе части в квадрат: 

.

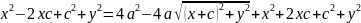
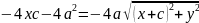Разделим обе части на ( 4): .

Возведем обе части в квадрат:



.

Разделим обе части на : .

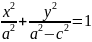. Обозначим:

(3) – каноническое уравнение эллипса, где .

II. График эллипса

1. Симметрия Из (3) получим, что эллипс имеет две оси симметрии – ось Ox и ось Oy; и центр симметрии – начало координат O (0;0).

2. В ершины эллипса Вершины эллипса – точки пересечения эллипса с осями симметрии, т .е. с осью Ox и осью Oy. – вершины эллипса. ,

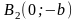
3. График эллипса .

Итак, – вершины эллипса, – фокусы эллипса.

def. Отрезок и его длина называется большой осью эллипса. Отрезок и его длина называется малой осью эллипса. 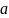– большая полуось, – малая полуось.