2.3. Задания для аудиторных занятий

Пример 1. Вычислить определители 2 -го порядка.

, ,

Пример 2 Дано 5 определителей. Используя свойства, найдите среди них: 1) равные по величине; 2) равные по величине, но противоположные по знаку; 3) равные нулю;

, , , ,

Подтвердите ответы простым вычислением

Пример 3. При каком значении определитель равен 0?

Пример 8. Вычислить определители по правилу Сарюса

1. 2. 3.

Пример 9. Вычислить определители методом разложения по элементам строки

4. 5. 6.

Пример 11. Вычислить определители, используя свойства:

10 11 12

3.Системы линейных алгебраических уравнений

3.1. Основные понятия и определения

Определение 1.Выражение вида

(1)

где – неизвестные; – коэффициенты при неизвестных, причем первый индекс обозначает номер уравнения, а второй – номер неизвестного; b_1, b_{2 .,…}b_n - свободные члены, называется системой линейных алгебраических уравнений (СЛАУ).

Определение 2. Набор чисел , обращающий каждое уравнение в тожество, называется решением системы.

Определение 3. Система называется совместной, если она имеет решение, и несовместной в противном случае..

Определение 4. Если система имеет единственное решение, то говорят, что она совместна и определена. Если система имеет бесконечное множество решений, то говорят – она совместна и не определена.

Определение 5.Две системы называются равносильными, если они имеют одинаковые множества решений.

Если в системе произвести элементарные преобразования, т.е. :

1. поменять местами два любых уравнения;

2. умножить (разделить) все члены любого уравнения на некоторое число k;

3. прибавить ко всем членам одного уравнения соответствующие члены другого уравнения, умноженные на некоторое число;

4. отбросить уравнения с нулевыми коэффициентами, или пропорциональными коэффициентам другого уравнения

- то исходная система уравнений приведется к равносильной.

Уравнения, входящие в систему, называются линейными, потому что неизвестные входят в нее в первой степени.

По внешнему виду системы, как и матрицы, могут быть квадратными, когда число уравнений совпадает с числом неизвестных (m=n), и прямоугольными, когда эти числа не совпадают.

Пусть А - матрица из коэффициентов при неизвестных, Х - матрица-столбец из неизвестных, В - матрица-столбец из свободных членов. Выражение АХ = В называется матричной записью системы «m» линейных уравнений с « n» неизвестными.

Действительно, произведение

= - это выражение, стоящее в левой части системы. Оно равно выражению, стоящему в правой части системы – матрице В: В = .

Поскольку 2 матрицы равны, когда равны элементы, стоящие на пересечении выбранных строк и столбцов, то вновь приходим к первоначальной системе:

Решение систем линейных уравнений методом Крамера

Рассмотрим систему двух линейных уравнений с двумя неизвестными:

(2)

Найдём её решение. Для этого первое уравнение умножим на a₂₂, а второе – на a_12. После сложения этих выражений и приведения подобных членов получим выражение:

., откуда (3)

Аналогично, умножив первое уравнение системы (2) на a₂₁, а второе на –a₁₁ и сложив их, получим

,

откуда (4)

Множитель, стоящий перед неизвестными x и y и в знаменателях полученных дробей нам уже встречался. Это определитель второго порядка.

.

Он составлен из коэффициентов при неизвестных и называется главным. Выражения, стоящие в правых частях и затем в числителях – тоже определители. Они получаются из определителя заменой первого и второго столбцов поочередно на столбец свободных членов и называются побочными:

_{И тогда выражения ( 3}) и (4) для решения системы запишутся в более компактной форме:

(5)

Их называют формулами Крамера

Пример 1. Решить систему уравнений методом Крамера:

Решение. Вычислим определители:

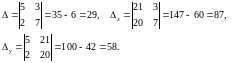
Используем формулы Крамера:

Сделаем проверку: 5·3 + 3·2 = 21, 2·3 + 7·2 = 20.

Ответ: х = 3, у = 2, или в матричной форме .

Пример 2. Решить систему

Решение. Найдем все определители:

,

Откуда - не существует, - не существует.

Ответ: система несовместна, т.к. главный определитель равен нулю, а остальные отличны от него.

Пример 3. Решить систему

Решение. Главный определитель равен нулю (см. пример 2.). Найдем побочные определители:

.

По формулам Крамера х = , у = .

Такие выражения называются неопределенными.

Найдем решение следующим образом. Поскольку второе уравнение пропорционально первому, то его можно отбросить. Остается только первое уравнение:

3х + 5у = 8. Откуда , или .

В обоих выражениях одна переменная выражается через другую, поэтому общее решение запишется в виде

или .

Если в последнем выражении положить у = 1, то получим частное решение . Давая переменной «у» другие значения, получим новые решения для неизвестной «х». В этом случае говорят, что система имеет множество решений, то есть совместна, но не определена.

Ответ: система совместна, но неопределенна. Её общее решение запишется в виде или

Итак, мы рассмотрели все варианты решения квадратных систем второго порядка методом Крамера. Сформулируем их в виде утверждений, доказательства которых очевидны.

1. Если главный определитель системы отличен от нуля – система имеет единственное решение (она совместна и определена).

2. Если главный определитель равен нулю, а побочные - нет, то система не имеет решения (она несовместна).

3. Если все определители системы равны нулю – система имеет множество решений (она совместна и не определена). В этом случае находят сначала общее решение, как показано в примере 3, а потом частное, удовлетворяющее условиям задачи.

Эти утверждения верны для квадратных систем любого порядка

Рассмотрим систему из 3-х уравнений с тремя неизвестными

Используя определители 3-го порядка, решение такой системы можно записать в таком же виде, как и для системы двух уравнений, т.е.

(6)

где

,

Такие же формулы верны для систем четвертого и более высокого порядков. Главный определитель всегда составлен из коэффициентов при неизвестных. Побочные получены из главного путем замены 1-ого (2-ого, 3-его поочередно) столбца на столбец свободных членов.

Пример 2. Решить систему линейных уравнений.

Решение. Находим главный определитель из коэффициентов при неизвестных.

Поскольку ¹ 0, то для нахождения решения системы можно применить метод Крамера. Составим и вычислим побочные определители:

Ответ: x=1, y=2, z= -1., или