
- •Лекция 4
- •4.1. Числовые ряды
- •4.2. Сходимость ряда
- •4.3. Необходимое условие сходимости ряда
- •4.4. Примеры числовых рядов
- •4.5. Обобщенно-гармонические ряды
- •4.6. Свойства сходящихся рядов
- •4.7. Остаток ряда
- •4.8. Знакоположительные ряды
- •4.8. Признаки сравнения
- •4.9. Признак Даламбера
- •4.10. Радикальный признак Коши
- •4.11. Знакопеременные ряды
- •4.12. Знакочередующиеся ряды
- •4.13. Оценка остатка сходящегося знакочередующегося ряда
Лекция 4
ЧИСЛОВЫЕ РЯДЫ, СХОДИМОСТЬ И СУММА РЯДА
4.1. Числовые ряды
Определение 4.1. Пусть задана числовая
последовательность
 .
Числовым рядом (или просто рядом)
называется выражение вида
.
Числовым рядом (или просто рядом)
называется выражение вида
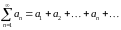 , (4.1)
, (4.1)
в котором элементы a1,
a2, a3,
..., an,
... – члены ряда, представляют собой
действительные числа соответствующей
числовой последовательности
,
где
 – общий член ряда.
– общий член ряда.
Многоточие, которое поставлено в конце выражения (4.1) указывает на то, что ряд содержит бесконечное число членов.
4.2. Сходимость ряда
Определение 4.2. Пусть дан ряд (4.1).
Частичной суммой
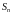 ряда называется сумма первых
ряда называется сумма первых
 членов ряда:
членов ряда:
 ,
где
,
где
 Образуем
последовательность частичных сумм
Образуем
последовательность частичных сумм
 ряда, полагая:
ряда, полагая:

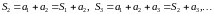 ,
, .
.
Определение 4.3.
Если существует конечный предел
последовательности частичных сумм
ряда (4.1), то говорят, что ряд (4.1) сходится,
а число
 называется его суммой. Если же
предела последовательности
не существует или он равен бесконечности,
то ряд (4.1) называется расходящимся.
называется его суммой. Если же
предела последовательности
не существует или он равен бесконечности,
то ряд (4.1) называется расходящимся.
Если ряд (4.1) сходится и имеет сумму S, то пишут
S = a1 + a2 + a3
+ ...или
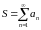 .
.
Если же ряд (4.1) расходится, то ему не приписывают никакого числового значения.
4.3. Необходимое условие сходимости ряда
Теорема 4.1. Общий член сходящегося
ряда при возрастании своего номера
стремится к нулю, т.е. если ряд (4.1)
сходится, то
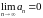 .
.
Доказательство. Из сходимости ряда
(4.1) следует, что
 ,
а также
,
а также
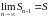 .
Тогда из определения частичных сумм
ряда:
.
Тогда из определения частичных сумм
ряда:
 ,
следует, что
,
следует, что
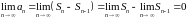 ,
что и требовалось.
,
что и требовалось.
Итак: для того, чтобы ряд сходился, необходимо, чтобы его общий член стремился к нулю; но этого еще – не достаточно для сходимости ряда. Если общий член ряда стремится к нулю, то ряд может, как сходиться, так и расходиться. Но если предел общего члена ряда не равен нулю, то ряд расходится. В случаях, когда общий член ряда стремится к нулю, для ответа на вопрос о сходимости ряда нужно использовать другие признаки.
4.4. Примеры числовых рядов
Пример 4.1. Рассмотрим ряд, состоящий из одних нулей: 0+0+0+….
Общий член этого ряда
 ,
предел общего члена ряда равен нулю.
Частичной суммой
ряда:
,
предел общего члена ряда равен нулю.
Частичной суммой
ряда:
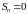 ,
предел последовательности частичных
сумм:
,
предел последовательности частичных
сумм:
 .
Следовательно, ряд сходится и сумма его
равна нулю.
.
Следовательно, ряд сходится и сумма его
равна нулю.
Пример 4.2. Рассмотрим ряд, состоящий из одних: 1+1+1+….
Общий член ряда
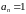 .
Не выполняется необходимое условие
сходимости ряда. Следовательно, ряд
расходится.
.
Не выполняется необходимое условие
сходимости ряда. Следовательно, ряд
расходится.
Пример 4.3. Рассмотрим ряд
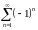 =
–1+1–1+1–1+….. .
=
–1+1–1+1–1+….. .
Общий член ряда принимает значение an= –1, если n – нечетное и an=1, если n – четное. Тогда частичные суммы ряда: Sn = –1, если n - нечетное, и Sn = 0, если n - число четное. Следовательно, не существует предел последовательности , значит, ряд расходится.
Пример 4.4. Рассмотрим ряд
 ,
который называется гармоническим рядом,
который расходится, а необходимое
условие сходимости выполняется:
.
,
который называется гармоническим рядом,
который расходится, а необходимое
условие сходимости выполняется:
.
Пример 4.5. Рассмотрим ряд
 .
Общий член ряда
.
Общий член ряда
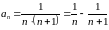 .
Тогда частичную сумму
можно представить в виде:
.
Тогда частичную сумму
можно представить в виде:
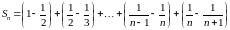 .
Раскрывая скобки, видно, что, начиная
во второго все слагаемые, кроме первого
и последнего уничтожаются. Получаем:
.
Раскрывая скобки, видно, что, начиная
во второго все слагаемые, кроме первого
и последнего уничтожаются. Получаем:
 .
Следовательно,
.
Следовательно,
 .
Получили: ряд сходится и сумма равна
1.
.
Получили: ряд сходится и сумма равна
1.
