ЛЕКЦИЯ 5

Предел функции

5.1. Предел функции в точке

Рассмотрим функцию , определенную в некоторой окрестности точки , за исключением, быть может, самой точки , т.е. Определение 5.1. Число называется пределом функции при , стремящимся к , если для любого положительного числа , как бы мало оно ни было, найдется такое положительное число , что для всех , удовлетворяющих неравенству: , будет справедливо неравенство .

Данное определение предела иногда называют определением пределом функции по Коши или определением на языке . Его кратко записывают следующий образом:

5.2 . Графический смысл предела функции в точке

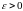Неравенство для всех точек , удовлетворяющих условию , эквивалентное неравенствам , справедливое для всех точек , таких, что: . Получили: , если для любого существует такая – окрестность точки : , за исключением, может быть самой точки : , что для всех из – окрестности точки , соответствующие значения функции попадают в – окрестности точки : .

Иными словами: число является пределом функции при , стремящимся к , если для любого положительного числа найдется такое положительное число , что все точки графика функции лежат на плоскости в прямоугольнике .

5.3. Предел функции по Гейне

Другое определение предела функции в точке может быть высказано в терминах пределов последовательностей.

Определение 5.2 (предела функции по Гейне). Число называется пределом функции при , стремящемся к , если она определена на некоторой окрестности точки , за исключением, быть может, самой точки , и если какова бы ни была последовательность , сходящаяся к точке такая, что для всех натуральных , соответствующая последовательность значений функции существует и сходится к числу . Это записывают, как .

Здесь считается, что последовательность пробегает значения, для которых определена функциональная последовательность значений функции .

Отсюда следует, в частности, что для любого существует такое , что для любой последовательности , сходящейся к , точки с координатами находятся на плоскости внутри прямоугольника, ограниченного прямыми: с боков и снизу и сверху

Теорема 5.1. Определения предела функции по Коши и Гейне эквивалентны.

Доказательство.

Пусть функция имеет предел при в смысле определения Коши, и переменная . Зададим любое как угодно малое положительное число , и подберем такое положительное число , что все точки произвольной последовательности , лежащие в области определения функции , начиная с некоторого номера , удовлетворяли неравенству: . Но тогда для всех . А это означает, что последовательность чисел стремится к . Но т.к. это свойство верно для любой сходящейся к последовательности , лишь бы и все точки последовательности принадлежали к области определения функции, то доказано, что из первого определения (5.1) предела следует второе (5.2).

Наоборот, пусть функция имеет предел в смысле второго определения (5.2). Допустим, противное: что функция не имеет предела в смысле первого определения (5.1). Это значит, что существует хотя бы одно положительное число , которое мы обозначим через , для которого нельзя подобрать такое положительное число , фигурирующее в определении 5.1. Таким образом, для любого положительное число , среди , удовлетворяющих соотношениям , должно найтись хотя бы одно такое, что для него .

В качестве возьмем все числа вида , где . Для каждого числа найдется такая точка ( ), для которой , но в то же время ( ).

Из этих соотношений видно, что нашлась такая последовательность , которая сходится к точке ( ), но в то же время последовательность не стремится к числу . Таким образом, предположение, что из второго определения предела (5.2) не следует первое (5.1) , привело к противоречию. Эквивалентность двух определений доказана.