Вычисление предела последовательности
Применяя
эту теоремы о бесконечно малых и о связи
бесконечно малых и бесконечно больших
последовательностей, можно находить
многие пределы.
Пример3.6.
Найдем предел последовательности с
общим членом
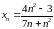 .
В числителе и знаменателе стоят многочлены
второй степени. Вынесем
.
В числителе и знаменателе стоят многочлены
второй степени. Вынесем
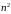 множителем,
как в числителе, так и в знаменателе, а
потом сократим дробь на
.
множителем,
как в числителе, так и в знаменателе, а
потом сократим дробь на
.
Представив
в
виде
 .
.
Установим,
что предел числителя и знаменателя
существует:
предел
числителя:
 ,
,
предел
знаменателя:
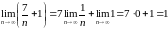 .
.
Поэтому,
получим:
 .
.
Рассмотрим
общий случай, когда последовательность
представляетсобой отношение двух
многочленов спепени
и
:
 .
Тогда
.
Тогда

14


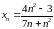 .
В числителе и знаменателе стоят многочлены
второй степени. Вынесем
.
В числителе и знаменателе стоят многочлены
второй степени. Вынесем
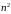 множителем,
как в числителе, так и в знаменателе, а
потом сократим дробь на
.
множителем,
как в числителе, так и в знаменателе, а
потом сократим дробь на
. .
. ,
,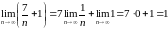 .
. .
. .
Тогда
.
Тогда