6. Фундаментальные последовательности

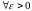
Определение 3.7. Последовательность называется фундаментальной (или последовательностью Коши, или последовательностью, сходящейся в себе), если N: 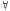n>N, p-натурального следует, что 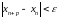(или ).

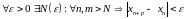Теорема 3.10 (Критерий Коши). Числовая последовательность сходится тогда и только тогда, когда она является фундаментальной.

Пример 3.3. Используя критерий Коши можно доказать, что последовательность не имеет предела . Очевидно, что , поэтому если выбрать = 1, то получим отрицание утверждения, что последовательность фундаментальна . А именно:

( ), : , : ( ) .

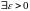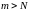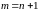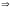
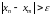Следовательно, последовательность не является фундаментальной и, поэтому не имеет предела.

Пример 3.4. Исследовать на сходимость последовательность , где общий член последовательности вычисляется по формуле:

Для любых натуральных чисел и рассмотрим модуль разности

= При 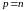получим, что

> . И если в качестве произвольного сколь угодно малого числа , взять , то получим, что последовательность не фундаментальна и, поэтому не имеет предела.

7. Монотонные последовательности

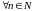
Определение3.8. Последовательность называется возрастающей, если , т.е. каждый член последовательности меньше последующего: x_n< .

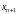Определение3.9. Последовательность называется убывающей, если 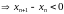, т.е. каждый член последовательности больше последующего: .

Определение3.10. Последовательность называется невозрастающей, если 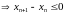, т.е. каждый член последовательности не меньше последующего: .

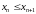Определение3.11. Последовательность называется неубывающей, если 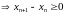, т.е. каждый член последовательности не больше последующего: .

Определение3.12. Последовательность называется монотонной, если она является или возрастающей, или убывающей, или невозрастающей, или неубывающей.

Теорема 3.11. У всякой возрастающей ограниченной сверху последовательности существует предел.

Теорема 3.12. У всякой убывающей ограниченной снизу последовательности существует предел.

Теорема 3.13. У всякой монотонной ограниченной последовательности существует предел.

Замечание 1. Условие ограниченности монотонной последовательности представляет собой необходимое и достаточное условие ее сходимости. Действительно, по теореме 3.9 сходящаяся монотонная последовательность ограничена.

Замечание 2. Сходящаяся последовательность может и не быть монотонной. Например, последовательность 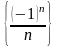сходится к числу ноль, но не является монотонной: .

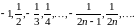8. Бесконечно малые и бесконечно большие последовательности

Определение 3.13. Последовательность 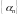называется бесконечно малой, если для любого положительного числа ε можно указать номер N такой, что при , все элементы этой последовательности удовлетворяют неравенству . Таким образом, бесконечно малая последовательность — это последовательность, предел которой равен нулю.

(Обычно, элементы бесконечно малой последовательности обозначаются малыми греческими буквами).

Теорема 3.14. Любая бесконечно малая последовательность является ограниченной.

Определение 3.14. Последовательность называется бесконечно большой, если для любого положительного числа A можно указать номер N такой, что при все элементы этой последовательности удовлетворяют неравенству .

Любая бесконечно большая последовательность является неограниченной. Но не каждая неограниченная последовательность является бесконечно большой. Например, неограниченная последовательность 1, 2, 1, 3, ... 1, n, ... не является бесконечно большой, так как при A > 1 неравенство не выполняется для с нечетными номерами

Бесконечно большая последовательность — это последовательность, предел которой равен бесконечности.

Теорема 3.15. Если — бесконечно малая последовательность, и 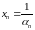, то последовательность — бесконечно большая. Наоборот: если – бесконечно большая последовательность, все отличны от нуля и , то последовательность – бесконечно малая.

Пример 3.5. Пусть , последовательность является бесконечно малой, 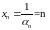. Тогда последовательность будет бесконечно большой.

Теорема 3.16. Сумма, разность и произведение конечного числа бесконечно малых последовательностей есть также бесконечно малая последовательность.

Теорема 3.17. Произведение бесконечно малой последовательности на ограниченную последовательность есть бесконечно малая последовательность

Теорема 3.18. Предел последовательности равен тогда, и только тогда, когда представимо в виде суммы , где – бесконечно малая.