ЛЕКЦИЯ 3

ПРЕДЕЛ ЧИСЛОВОЙ ПОСЛЕДОВАТЕЛЬНОСТИ,

ЕГО СВОЙСТВА И ВЫЧИСЛЕНИЕ

1. Определение числовой последовательности

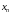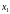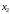Под числовой последовательностью понимается результат последовательного выбора элементов из заданного числового множества. Числовая последовательность считается заданной, если указан закон или правило, по которому каждому натуральному числу ставится в соответствие элемент заданного числового множества. Элементы называются членами последовательности: – первым членом, – вторым, – -ым или общим членом последовательности. Последовательность записывается в виде , или . Числовая последовательность является функцией натурального аргумента: .

Из школьного курса известны примеры числовых последовательностей. Это арифметическая и геометрическая прогрессии:

арифметическая прогрессия – это такая числовая последовательность, в которой каждый её член равен предыдущему, сложенному с постоянным для данной последовательности числом: 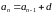, где – формула общего члена, 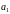– первый член прогрессии, а число называется разностью прогрессии;

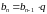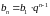геометрическая прогрессия – это числовая последовательность, в которой каждый её член равен предыдущему, умноженному на постоянное для данной последовательности число: , где – формула общего члена, 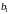– первый член прогрессии, а число 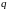называется знаменателем прогрессии.

2. Задание числовой последовательности

Числовую последовательность чаще всего задают аналитическим способом. Это осуществляется с помощью формулы, задающей -й член последовательности через его номер . Например, 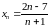. По этой формуле

можно вычислить любой член последовательности:

Другой способ задания числовой последовательности – рекуррентный (от латинского слова «recurrens», что значит – «возвращающийся»). В этом способе задают несколько первых членов последовательности, а также правило, позволяющее вычислять каждый следующий член через известные предыдущие. Например: 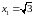и . Тогда можно найти , .

3. Предел числовой последовательности и его геометрический смысл

Рассмотрим поведение членов последовательности при неограниченном возрастании номера (это означает, что и читается: « стремится к бесконечности»).

Определение 3.1. (определение предела последовательности). Число а называется пределом последовательности , если для любого положительного числа можно указать такой номер (натуральное число) (N зависит от ), что при всех номеров выполняется неравенство (модуль разности -ого члена последовательности и числа меньше ). Это записывают 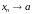или ( – три первые буквы латинского слова «limes» – «предел»). Кратко это можно записать с помощью логической символики следующим образом:

.

Геометрический смысл определения предела последовательности заключается в том, что независимо от малости интервала с центром в точке все члены последовательности с номерами, большими некоторого числа 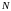, будут находиться в этом интервале; а вне указанного интервала может находиться лишь конечное число членов последовательности. Это следует неравенство эквивалентно неравенству

, которые справедливы для всех членов последовательности с номерами , где число определяется наперед заданным сколь угодно малым положительным числом . В этом случае точка называется предельной точкой последовательности .

Последовательность может иметь несколько предельных точек.

Пример3.1 последовательности, имеющей две предельные точки. Последовательность имеет две предельные точки 0 и 2.

Если все члены последовательности принимают одно и то же числовое значение, то предел этой последовательности равен этому значению.

Пример3.2. Последовательность 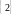, элементами которой являются числа 2,2,2,..., имеет предел 2. В самом деле,

, последнее неравенство выполняется, начиная с первого члена, т.к. .

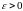Не у всякой последовательности существует предел. Например, если взять последовательность 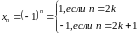, то у неё не будет предела. Ее члены попеременно равны и , и не стремятся ни к какому пределу.

Определение 3.2. Последовательность называется сходящейся, если у неё существует единственный конечный предел, и называется расходящейся, если нет предела. В общем случае пределов может быть несколько.

В определении 3.1 число ассоциировалось с конечным числом. Но определение предела можно расширить и на бесконечные значения: и . Например,

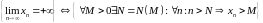– предел последовательности равен , если для любого сколь угодно большого положительного числа найдется такое натуральное число , что все члены последовательности с номерами большими, чем , будут больше заданного числа .

– предел последовательности равен , если для любого сколь угодно большого положительного числа найдется такое натуральное число , что все члены последовательности с номерами большими, чем , будут меньше, чем число .

Термин «сходящаяся последовательность» не распространяется на последовательности с бесконечными пределами.

Пример сходящейся последовательности: последовательность 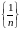называется гармонической; её предел равен нулю, она состоит из элементов