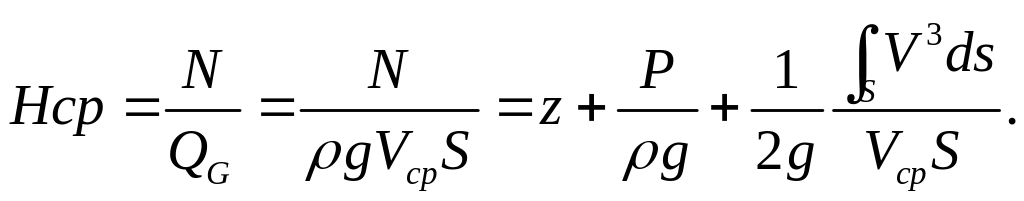6. Динамика вязкой жидкости

1. Отличия моделей реальной вязкой жидкости от идеальной.

2. Мощность потока.

3. Коэффициент Кориолиса.

4. Энергобаланс потока.

5. Режимы движения жидкости.

6. Гидравлические потери: местные и на трение.

7. Принцип Вентури и его применение.

6.1. Отличия реальной (вязкой) жидкости от идеальной.

В идеальной жидкости работа сил, действующих на жидкость, полностью идет на изменение ее кинетической энергии, происходит преобразование кинетической энергии в потенциальную и наоборот.

В реальной жидкости часть работы теряется при преобразовании кинетической энергии в потенциальную из-за наличия сил трения. Возникают потери, эти потери необратимы.

Модель несжимаемой реальной жидкости учитывает влияние вязкости в виде:

1) потерь энергии потока;

2) неравномерности распределения скоростей слоев жидкости по сечению трубопровода.

Уравнения движения вязкой жидкости очень сложны и даже для простейших случаев решаются с помощью численных методов.

Для инженерных задач при изучении движения вязких жидкостей применяется метод усреднения характеристик потока, который позволяет учесть потери энергии, связанные с вязкостью.

При движении вязкой жидкости происходит торможение потока. В эпюре скоростей наибольшие значения достигаются в центральной части потока, а по мере приближения к стенке скорость уменьшается до нуля. Пример распределения скоростей в сечении показан на рис. 6.1.

Рис.6.1 Эпюра скоростей в потоке реальной жидкости

Происходит скольжение или сдвиг одних слоев по другим и между слоями возникают касательные напряжения. Движение вязкой жидкости сопровождается вращением частиц, вихреобразованием и перемешиванием.

При движении реальной жидкости преодоление сопротивлений, связанных с вязкостью, требует затрат энергии, поэтому удельная энергия движущейся вязкой жидкости не остается постоянной, как в случае идеальной жидкости, а уменьшается вдоль потока.

Определить мгновенные скорости в различных точках сечения потока реальной жидкости сложно, поэтому рассматривают средние скорости, которые проще измерить.

При выводе уравнения Бернулли для потока реальной вязкой жидкости делают следующие допущения.

1) Рассматривают средние скорости и средние значения удельной энергии жидкости в данном сечении, то есть проводят осреднение характеристик потока.

2) Принимают, что в пределах рассматриваемых поперечных сечений потока, справедлив основной закон гидростатики, считают гидростатический напор величиной постоянной для всех точек данного сечения.

6.2. Мощность потока

Для усреднения характеристик вводится понятие мощности потока.

Мощность - отношение работы, выполненной за определенный промежуток времени к длительности этого промежутка.

Мощностью потока называется полная энергия, которую проносит поток через данное сечение в единицу времени.

Рассмотрим определение мощности потока на примере потока, поступающего в гидроцилиндр (рис.6.2).

Работа, совершаемая потоком, определяется, как произведение силы на перемещение. Сила давления жидкости это произведение давления р. на площадь S гидроцилиндра, перемещение - это ход поршня - L под действием этой силы.