4.4. Определение уравнения поверхности равного давления и давления в любой точке при равномерном вращении сосуда с жидкостью

При вращении открытого цилиндрического сосуда с жидкостью с постоянной угловой скоростью ω вокруг вертикальной оси силы трения о стенки вращающегося сосуда будут увлекать за собой жидкость. Она постепенно приобретет угловую скорость сосуда, находясь по отношению к сосуду в покое. Свободная поверхность жидкости изменится.

В центральной части уровень жидкости опустится, у стенок она поднимется, и вся свободная поверхность жидкости станет поверхностью вращения (рис.4. 3). Проведем координатные оси, ось Z по оси вращения, а перпендикулярные ей оси Х и У по дну сосуда.

Рассматривая равновесие частицы жидкости, приложим к ней единичные массовые силы в виде g - ускорения силы тяжести и ω²r - центробежного ускорения.

Определение уравнения поверхности. Проекции этих единичных массовых сил на оси

X = ω²r Cos(r^x)= ω²X

Y = ω²r Cos(r^у)= ω²Y,!

Z = -g.

Обозначения Х и Н одинаковые!

Подставляя проекции в уравнение поверхности равного давления

X*dх+У*dy+Z*dz = 0,

ω²*X*dх + ω²*Y*dy – g*dz = 0.

и интегрируя, получим (ω²/2) (X² + Y ²) – gZ +С = 0,

Рис.4.3. Относительный покой жидкости во вращающемся сосуде.

При начальных условиях в вершине параболоида свободной поверхности X =Y = 0, z= Z₀, z= Z₀, С = gZ₀.

(ω²/2)*(X² + Y ²) – gZ + gZ₀ = 0,

(ω²/2)*(X² + Y ²) =g(Z -Z₀),

а после деления на g получаем уравнение свободной поверхности

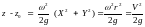(4.20)

Высота параболоида, получается из этой формулы

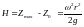
Поверхности равного давления образуют семейство параболоидов, сдвинутых по вертикальной оси. Каждому значению р на оси соответствует свой параболоид, положение которого определяют начальные условия.

Эти поверхности будут конгруэнтными относительно оси Oz, то есть их можно совместить, изменив их положение в пространстве.

Определение давления в любой точке. Подставим проекции единичных массовых сил в дифференциал давления

dp = ρ(Xdx + Ydy + Zdz) = ρω² (Xdx + Ydy) –ρgdz,

вынесем знак дифференциала за скобки,

dp = ρ* d[(ω²/2) (X² + Y²)] –ρ gdz, проинтегрировав, получим

p = ρ(ω²/2) (X² + Y²) –ρ gz + С₁, (4.21)

Определим С₁ при начальных условиях, соответствующих вершине параболоида свободной поверхности Р = Р₀, x=y=0, z = z₀ , тогда С₁ = Р₀ + ρgz₀, подставим С₁ в (4.21) получим уравнение для определения давления в любой точке

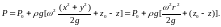(4.22)

При z₀=0, Р₀=0, когда параболоид касается дна

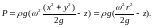
4.5 Свойства параболоида вращения

Высота параболоида может быть определена по формуле

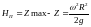
Объем параболоида, касающегося дна равен половине объема цилиндра с радиусом основания R и высотой Н, такой же объем занимает пространство W’ под параболоидом (рис.4.5а)

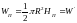
Рис.4.5. Соотношение объемов в параболоиде, касающемся дна.

Wп- объем параболоида,W’ – объем под параболоидом, Hп – высота параболоида

Рис.4.6. Соотношение объемов в параболоиде, касающемся краев цилиндра Hп – высота параболоида., R – радиус сосуда, W1 –объем под высотой жидкости в сосуде до начала вращения, W2 - объем над высотой жидкости, z₀ – положение вершины параболоида, Н - высота жидкости в сосуде до начала вращения.

На рис.4.6а уровень жидкости в цилиндре до начала вращения Н. Объем жидкости Wж до и после вращения сохраняется и равен сумме объема Wц цилиндра с высотой z₀ плюс объем жидкости под параболоидом, который равен объему параболоидаWп с высотой Нп

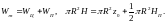
Если параболоид касается стенок цилиндра, высота жидкости в цилиндре до начала вращения Н делит высоту параболоида Нп на две равные части, нижняя точка (вершина) параболоида расположена по отношению к основанию

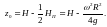
Кроме того, высота Н делит параболоид на две части (рис.4.6в), объемы которых равны W₂=W₁. Из равенства объемов параболического кольца W₂ и параболической чашки W₁, рис.4.6в

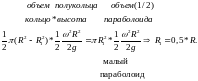
При пересечении поверхностью параболоида днища сосуда (рис.4.7) W₁=W₂=0,5W_кольца

Рис.4.7 Объемы и высоты при пересечении поверхностью параболоида днища цилиндра

Высоты на рис.4.6

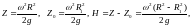
объемы на рис.4.6 .
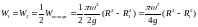