Лекция 4-я, осень 2017.
4. Гидростатика-3
Вопросы к лекции:
1. Относительный покой жидкости .Прямолинейное движение с постоянным ускорением. Определение давления в любой точке.
2. Прямолинейное движение с постоянным ускорением. Определение положения свободной поверхности при движении сосуда.
3. Вращение сосуда с постоянной угловой скоростью. Определение положения свободной поверхности при равномерном вращении сосуда с жидкостью.
4. Вращение сосуда с постоянной угловой скоростью. Определение давления в любой точке.
5. Вращение сосуда с постоянной угловой скоростью. Определение силы давления жидкости на дно, крышку, стенку.
6. Вращение сосуда с постоянной угловой скоростью. Свойства параболоида.
7. Вращение сосуда с постоянной большой угловой скоростью.
4. Относительный покой жидкости.
4.1. Прямолинейное равноускоренное движение сосуда с жидкостью.
При прямолинейном движении цистерны с жидкостью на частицы жидкости, кроме сил тяжести действуют силы инерции, при этом поверхность жидкости принимает новое положение равновесия - положение относительного покоя.
Относительным покоем называется состояние равновесия жидкости под действием сил тяжести и инерции в подвижном сосуде.
При относительном покое свободная поверхность жидкости и поверхности равного давления, занимают положения, отличающиеся от положения в неподвижном сосуде.
Основное свойство поверхностей равного давления: равнодействующая массовых сил всегда нормальна к ним.
Дифференциал давления
dP = ρ(X*dх+У*dy+Z*dz), (4.1)
Х,У,Z –проекции на оси координат единичных массовых сил или что то же ускорений массовых сил.
Вдоль поверхностей изменение давления равно нулю, так как это поверхности равного давления. Дифференциальное уравнение поверхности равного давления:
X*dх+У*dy+Z*dz = 0, dP=0. (4.2),
Этот трехчлен (4.2) определяет элементарную работу единичных массовых сил X,У,Z на перемещениях dх, dy, dz.
Из равенства нулю dР=0 следует, что работа элементарных массовых сил вдоль поверхности равного давления равна нулю, следовательно силы перпендикулярны перемещениям.
В состоянии относительного покоя результирующее ускорение (единичная массовая сила) перпендикулярна к поверхности равного давления.
Первый случай относительного покоя: сосуд, движущийся прямолинейно и равноускорено.
Второй случай: сосуд, вращающийся вокруг вертикальной оси с постоянной угловой скоростью.
На рис.4.1 сосуд движется с ускорением а по плоскости, наклоненной под углом α к горизонту. Оси координат связаны с движущимся телом. Рассматриваем равновесие частицы жидкости c массой δm, располагающейся на поверхности жидкости на оси симметрии сосуда. К этой частице привязаны ускорения. Можно рассматривать любую частицу жидкости, вся жидкость находится под действием массовых сил (в поле действия массовых сил).
Рис.4.1 Силы, действующие на жидкость при прямолинейном движении по плоскости с ускорением а; а) движение сосуда с ускорением вверх и направо, б) план ускорений для частицы. α – угол наклона плоскости,β – угол поворота свободной поверхности, g-ускорение свободного падения, j-ускорение силы инерции, q – суммарное ускорение, В– ширина сосуда, Н-высота жидкости в сосуде при горизонтальном его положении, Z,Х – проекции суммарного ускорения на оси Z и X, связанные с неподвижной плоскостью.
При относительном покое жидкость движется вместе с сосудом. Это состояние относительного равновесия.
В соответствии с аксиомами динамики уравнение движения материальной точки имеет вид
,
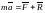(4.3)
где F- равнодействующая активных сил, R- равнодействующая реакции связей, a – абсолютное ускорение точки. Это уравнение можно переписать в виде
,
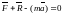(4.4)
где (ma) обозначают Ф и называют даламберовой силой инерции или просто силой инерции. Основное уравнение динамики приобретает вид
,
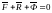(4.5)
где Ф – сила инерции.
Силы образуют сходящуюся систему сил и это уравнение можно рассматривать, как условие равновесия.
Принцип Даламбера: при движении материальной точки в любой момент времени приложенные к ней активные силы и реакции связей вместе с силой инерции образуют систему сил, эквивалентную нулю. В формулировке принципа речь идет об уравновешенности системы сил, а не равновесии материальной точки.
Дополняя систему активных сил и реакции связей , приложенных к точке, силой инерции, получаем систему сходящихся сил, для которой должно выполняться условие равновесия.
Для выяснения условий равновесия системы рассматриваются силы, действующие на частицу. На частицу жидкости массой δm действует суммарная массовая сила F, проекции которой на оси Fx, Fy, Fz
F = Fx+Fy+Fz = δm*а, (4.6)
где а – постоянное ускорение.
Поделив суммарную массовую силу на массу частицы δm, получим элементарную массовую силу F/δm и ее проекции на оси: Ох, Оу, Oz, Х= Fx/δm, У =Fу/δm и Z = Fz/δm.
F/δm = Fx/δm +Fy/δm +Fz/δm = X +Y + Z = а. (4.7)
Все составляющие этих сумм являются векторными величинами.
Проекции массовых сил, действующие на выделенный объем в направлении координатных осей, будут равны произведениям проекций единичных сил, умноженным на массу выделенного объема.
Fx = δmX, Fy = δmY, Fz = δmZ. (4.8)
Этими силами для системы на рис.4.1. являются силы инерции и тяжести.
В соответствии с принципом Даламбера, прикладываем к массе частицы единичные силы инерции j и тяжести g.
Единичная сила инерции j = - a направлена в сторону противоположную ускорению а (рис.4.1). Суммарная единичная массовая сила q, действующая на частицу жидкости, будет суммой векторов сил инерции j и силы тяжести g.