Теорема сложения ускорений при сложном движении точки
Эта теорема устанавливает связь между абсолютным, относительным и переносным ускорениями точки при сложном движении. Ее называют теоремой Кориолиса по имени доказавшего ее французского ученого.
Теорема Кориолиса
Абсолютное ускорение точки при сложном движении равно геометрической сумме относительного, переносного и кориолисова ускорений.
Доказательство
Запишем полученную при доказательстве теоремы сложения скоростей формулу (33) в виде:
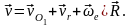
Вычислив полную производную по времени от обеих частей этого равенства, получим
(35)
В этой формуле полная производная от абсолютной скорости равна абсолютному ускорению
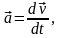
а
полные производные от векторов
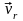и
,
заданных в подвижной системе координат,
следует вычислить по формуле Бура:
Тогда выражение (35) перепишется в виде
Учитывая, что локальная производная от относительной скорости равна относительному ускорению
раскрывая скобки и приводя подобные члены из последнего выражения получим
(36)
Если мысленно
остановить относительное движение,
положив
,
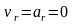то из формулы (36) получим выражение для
переносного ускорения:
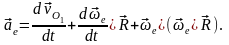
После этого выражение (36) можно переписать в виде
(37)
где
(38)
ускорение Кориолиса.
Теорема полностью доказана. Она выражается векторным равенством (37).
Поясним далее физический смысл и методы вычисления векторов в правой части равенства (37).
Относительное ускорение характеризует изменение вектора относительной скорости за счет относительного движения. Для его вычисления надо мысленно остановить переносное движение и представить себе, что точка движется по относительной траектории. В зависимости от вида относительной траектории относительное ускорение может иметь одну или две составляющих (см. рис. 24).
Рис. 24
Переносное ускорение характеризует изменение вектора переносной скорости за счет переносного движения. Для его вычисления надо мысленно остановить относительное движение и представить себе, что точка движется по переносной траектории. В зависимости от вида переносной траектории переносное ускорение тоже может иметь одну или две составляющих (см. рис. 25).
Рис. 25
Ускорение Кориолиса характеризует изменение вектора относительной скорости за счет переносного движения, а также изменение вектора переносной скорости за счет относительного движения. В соответствии с формулой (38) величина кориолисова ускорения может быть вычислена как модуль векторного произведения:
(39)
где
- модуль переносной угловой скорости
(угловой скорости подвижной системы
координат),
- модуль относительной скорости точки,
α – угол между векторами
и
Направление ускорения Кориолиса можно определить по правилу векторного произведения. Для этого нужно в рассматриваемой точке, совершающей сложное движение, построить векторы и , провести перпендикуляр к плоскости указанных векторов и направить ускорение Кориолиса вдоль этого перпендикуляра по правилу правого винта, поворачивая винт в сторону кратчайшего совмещения вектора с вектором (см. рис. 26).
Рис. 26
Направление
ускорения Кориолиса можно также
определить по правилу Жуковского. Для
этого нужно спроецировать вектор
на плоскость, перпендикулярную вектору
,
и повернуть полученную проекцию в
указанной плоскости на угол
в направлении переносного вращения
(см. рис. 27).
Рис. 27
Отметим особо частные случаи, когда ускорение Кориолиса обращается в нуль:
при
,
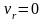т. е. в те моменты времени, когда
относительная скорость
равна нулю;
2)
при
,
т. е. если подвижная система координат
движется поступательно;
3)
при
,
т. е. если относительная скорость
параллельна оси переносного вращения.
Пример 5
Прямолинейная
трубка прикреплена к вертикальной оси
под углом
и вращается вокруг нее по закону
.
Вдоль трубки по закону
движется шарик М (см. рис. 28). Положительное
направление отсчета угла
показано на рисунке дуговой стрелкой,
считается положительным вниз по трубке
от точки О. Требуется определить величину
абсолютного ускорения точки М в момент
времени
Рис. 28
Решение
Мысленно свяжем подвижную систему координат с трубкой. Тогда переносным движением будет вращение трубки вокруг вертикальной оси, а относительным движением будет прямолинейное движение шарика вдоль трубки.
Определим сначала положение шарика в трубке в момент Для этого вычислим
Отложим полученное расстояние от точки О в положительном направлении отсчета . Проведем через найденное положение шарика относительную и переносную траектории (см. рис. 29).
Запишем теперь выражение для абсолютного ускорения точки М в соответствии с теоремой сложения ускорений:
(40)
В
связи с тем, что переносная траектория
окружность, переносное ускорение здесь
разложено на нормальную и тангенциальную
составляющие. Вычислим далее величину
каждого из векторов в правой части
выражения (40) для момента времени
и изобразим эти векторы на рис. 29.
Рис. 29
Относительное ускорение имеет только тангенциальную составляющую, так как траектория относительного движения прямая линия. Его алгебраическое значение равно
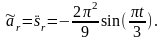
В
момент времени
Следовательно, для величины относительного
ускорения имеем
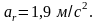Знак алгебраического значения показывает,
что вектор
направлен в сторону отрицательных
значений
Изобразим вектор
на
рис. 29.
Вычислим теперь для момента времени составляющие переносного ускорения:
Здесь
Покажем
на рис. 29 вектор
направив его к центру кривизны переносной
траектории. Так как
то переносное угловое ускорение
будет направлено в сторону положительного
направления отсчета угла
и вектор
следует направить по касательной к
переносной траектории в направлении
(см. рис. 29).
Определим теперь величину и направление ускорения Кориолиса для момента времени . Для этого момента времени алгебраическое значение переносной угловой скорости будет равно
Поэтому угловая переносная скорость будет направлена в сторону отрицательных значений угла и вектор будет направлен вниз вдоль оси переносного вращения (см. рис. 30). Алгебраическое значение относительной скорости для момента времени
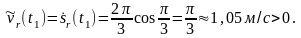
Следовательно, вектор направлен вдоль относительной траектории в сторону положительных значений . Для модуля ускорения Кориолиса получим
В
соответствии с правилом векторного
произведения вектор
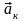будет направлен перпендикулярно
плоскости рисунка вдоль оси x.
Покажем этот
вектор на рис. 29 и 30.
Рис. 30
Для нахождения абсолютного ускорения точки выберем в точке М оси декартовой системы координат и запишем векторное равенство (40) в проекциях на эти оси:
Через найденные проекции величину абсолютного ускорения вычислим по формуле
