Задание движения точки естественным способом
В этом случае должны быть заданы (рис. 6):
траектория точки,
начало отсчета дуговой координаты s (точка О) на траектории и положительное направление её отсчета,
кинематическое уравнение движения в виде
s=f(t). (9)
Рис. 6
При данном способе задания движения точки используется естественная система координат, начало которой связано с движущейся точкой (рис. 7). Эта система координат имеет следующие оси:
касательная к
траектории (
);
главная нормаль (n), проходящая через центр кривизны траектории;
бинормаль (b).
Рис. 7
Найдем вектор скорости:
где
как
предел отношения бесконечно малой дуги
к стягивающей её хорде. Направление
вектора
установим с учетом того, что вектор
направлен по
при Δs>0
и противоположно
при Δs<0,
т. е. вектор
по хорде в сторону возрастания дуговой
координаты s.
Следовательно, единичный вектор
направлен по касательной к траектории
в направлении оси τ. Обозначим этот орт
оси τ через
.
Тогда для скорости точки получим
(10)
где
– проекция вектора скорости на ось τ,
называемая алгебраической скоростью.
Для модуля скорости в данном случае
справедлива формула
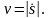
Прежде чем находить ускорение точки, выведем одну вспомогатель-ную формулу для производной от вектора постоянного модуля по скаляр-ному аргументу.
Рассмотрим вектор
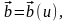где u
– некоторый скалярный аргумент. Пусть
вектор
имеет постоянный модуль
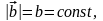то есть может изменять только своё
направление. По определению производной
Для
определения
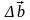из точки О отложим векторы
и
(рис. 8) и
соединим
их концы А и В. Угол поворота вектора
обозначим
.
Из равнобедренного треугольника АОВ
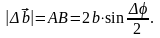
Для модуля искомой производной получим:
Отметим,
что
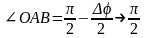при
Следовательно,
вектор
направлен перпендикулярно к
дифференцируемому вектору
в сторону его поворота при изменении
аргумента u
(рис. 8).
Рис. 8
Окончательно получим формулу
(11)
где
– единичный вектор, совпадающий по
направлению с вектором
Если скалярным аргументом является время t, то
Правую часть этой формулы можно записать в виде векторного произведения двух векторов:
(12)
где
– угловая скорость поворота вектора
.
Величина угловой скорости
Вектор
следует направить перпендикулярно
плоскости, в которой расположены векторы
и
,
в ту сторону, откуда поворот вектора
виден против часовой стрелки.
Определим теперь ускорение точки как производную от вектора скорости по времени, продифференцировав выражение (10):
Преобразуем
выражение для производной
с использованием формулы (11):
Здесь
кривизна траектории
выражена через радиус кривизны
.
Окончательно для ускорения точки получим
векторную формулу
(13)
Отсюда следует, что вектор ускорения точки имеет следующие проекции на оси естественной системы координат:
- проекция ускорения
на касательную к траектории, характеризующая
изменение вектора скорости по величине;
– проекция ускорения
на главную нормаль (нормальное ускорение),
характеризующая изменение вектора
скорости по направлению;
– проекция ускорения
на бинормаль, равная нулю при любом
движении точки.
Величину
,
которая может быть как положительной,
так и отрицательной, обычно называют
алгебраическим значением тангенциального
(касательного) ускорения, а величину
называют тангенциальным (касательным)
ускорением.
Модуль ускорения вычисляется по формуле
(14)
Все найденные выше характеристики движения точки показаны на рис. 9.
Рис. 9
Если
векторы
и
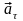направлены в одну сторону, то движение
точки называется ускоренным. В противном
случае движение точки называют
замедленным.
Отметим, что тангенциальное ускорение можно найти и при задании движения точки в декартовых координатах:
или
(15)
Найденное
по формуле (15) алгебраическое значение
тангенциального ускорения может быть
как положительной, так и отрицательной
величиной. При этом
соответствует ускоренному, а
– замедленному движению точки.
Путь, пройденный
точкой за промежуток времени
,
может быть вычислен по формуле
(16)
Далее рассмотрим кратко простейшие случаи движения точки. К ним относятся равномерное и равнопеременное движения.
Признаком
равномерного движения является
.
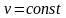В этом случае при выборе начала отсчета
дуговой координаты в начальном положении
точки (при t=0)
и положительного направления ее отсчета
в направлении скорости получим
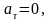
Признаком
равнопеременного движения является
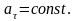В этом случае при том же выборе начала
отсчета и положительного направления
отсчета дуговой координаты получим
где
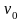– начальная скорость точки,
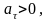знак « + » соответствует равноускоренному
движению, знак « − » – равнозамедленному.
Пример 2
Движение точки задано кинематическим уравнением
где s измеряется в метрах, а t – в секундах. Требуется определить путь, пройденный точкой за 4 секунды после начала движения.
Решение
Вычислим сначала производную
Далее по формуле (16) имеем
Чтобы избавиться от модуля под знаком интеграла, построим график функции на рис. 10.
Рис. 10
Теперь можно опустить модуль под знаком интеграла, разбив промежуток интегрирования на две части, и провести вычисления:
(м).