Глава 6. Уравнения равновесия

6.1. Независимые уравнения равновесия для различных систем сил

Если твердое тело под действием некоторой системы сил находится в равновесии, то для этой системы сил главный вектор и главный момент, вычисленный относительно произвольной точки О, равны нулю. Тогда из (69), (70) получим уравнения равновесия системы сил в векторной форме:

(71)

(72)

Если векторные равенства (71), (72) записать в проекциях на выбранные оси координат, то из двух векторных уравнений получим 6 алгебраических уравнений равновесия:

(73)

В формулах (73) суммирование производится для всех сил системы, но для краткости записи у знака суммы не указаны границы изменения индекса суммирования k. Будем использовать такое упрощение записи и в дальнейшем.

Отметим, что записанные выше уравнения равновесия (73) являются независимыми только для систем сил наиболее общего вида – пространственных произвольных. Для более простых систем сил независимых уравнений равновесия будет меньше шести. Ниже в таблице приведены независимые уравнения равновесия для систем сил различного вида. Эти независимые уравнения помечены в таблице знаком (+). Отметим, что для плоских систем сил, расположенных в плоскости Oxy, вычисление моментов сил относительно оси z эквивалентно вычислению алгебраических моментов сил относительно точки, выбранной в плоскости Oxy.

Уравнения равновесия Вид системы сил								Кол-во незави-симых ур-ий
Простран-ственная	Произвольная	+	+	+	+	+	+	6
	Параллельная ( )	–	–	+	+	+	–	3
	Сходящаяся	+	+	+	–	–	–	3
Плоская (в пл-ти OXY)	Произвольная	+	+	–	–	–	+	3
	Параллельная ( )	–	+	–	–	–	+	2
	Сходящаяся	+	+	–	–	–	–	2

Таблица 1. Независимые уравнения равновесия для различных систем сил

Докажем одну важную теорему статики.

Теорема Вариньона

Если система сил имеет равнодействующую, то векторный момент равнодействующей силы относительно какого-либо центра равен геометрической сумме векторных моментов всех сил системы, вычисленных относительно того же центра.

Доказательство

Пусть на твердое тело действует система сил , имеющая равнодействующую (см. рис. 78)

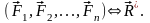
Рис. 78

Добавим к заданной системе сил уравновешивающую силу 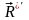, равную по величине, противоположно направленную и имеющую общую линию действия по отношению к равнодействующей силе . Тогда полученная система сил будет эквивалентна нулю

и должна удовлетворять уравнениям равновесия. В частности, сумма векторных моментов сил этой системы относительно любой точки О равна нулю:

но

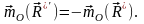
Тогда из предыдущей формулы получим

откуда следует утверждение теоремы:

Отметим, что аналогичное утверждение справедливо для алгебраических моментов и моментов сил относительно осей.