12.2. Объемный резонатор из отрезка прямоугольного волновода (частичная задача)

Берём стандартный, прямоугольный волновод с волной .

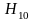Рассмотрим прямоугольный волновод сечением .

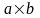Рис.12.6 Прямоугольный волновод

Определим структуру поля и параметры электромагнитных колебаний, возникающих в таком резонаторе.

z=0, z=l

H₁₀

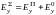
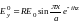
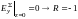
При наличии КЗ, в стенке появится отражённая волна.

По определению, продольно-волновое число . Для его определения воспользуемся граничной задачей.

,

;

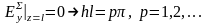
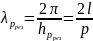
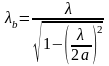учитывая это, можно написать:

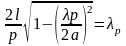
- длина волны резонансная, в свободном пространстве.

Индекс “p”, имеет простой физический смысл. Он показывает, число стоячих полуволн, вдоль оси резонатора.

Рассматриваемый тип колебаний имеет следующую аббревиатуру .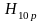

До образования резонатора в волноводе существовала волна .

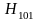- в таком резонаторе одна полуволна.

12.3. Тип колебаний: h10p Структура поля: h101

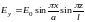- так обозначим “y” компоненту.

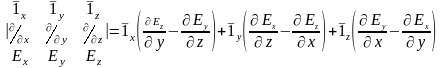
имеется только 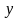составляющая.

]

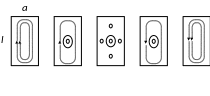
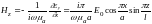Магнитное поле

Магнитного поля нет

Магнитное поле

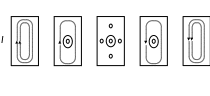
Рис.12.7 Структура поля H₁₀₁

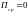
Поверхностные токи:

Из выражений для составляющих поля следует, что E и H отличаются на 90°, что свидетельствует о нулевом значении среднего за период вектора Пойнтинга и существовании в резонаторе колебательного процесса.В ходе этого процесса, дважды за период, энергия электрического поля преобразуется в магнитное и наоборот.

12.4. Общая задача о колебаниях в прямоугольном резонаторе. Классификация типов волн

E_ши

Рис. 12.8. Прямоугольный резонатор

Определим совокупность резонансных частот всех возможных типов колебаний, существующих в прямоугольном резонаторе с размерами . Введём декартову систему координат, при этом пусть размер совпадает с осью .

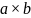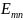Пусть в поперечном сечении с размерами структура поля совпадает со структурой поля волны . Резонансная длина волны, связана с длиной волны в волноводе с размерами дисперсионным уравнением.

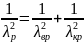
Полагая, если структура колебания в поперечном сечении резонатора, с размерами совпадает с поперечной структурой волны H_mn в прямоугольном волноводе, то мы получим уравнение:

Из рассмотренных в предыдущих параграфах следует, что случай H в прямоугольном волноводе, по крайней мере, один может принимать.

Из h следует, что индексы mn входят в это соотношение совершенно равноправно. Рассмотрим возможность, при которой индекс p соответствует нулевому значению.

p=0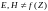

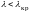
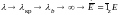
E₁₁₀

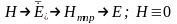
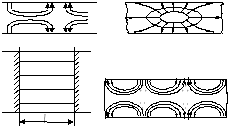
Рис. 12.9. Структура поля Е₁₁₀ в объемном резонаторе

Если мы поставим две металлические плоскости на расстоянии l, ненулевые индексы m и n на этих плоскостях будут удовлетворяться механически. Структура поля остается неизменной (какой была в отсутствии плоскостей).

В случае H_mn один из индексов может быть не равен нулю. В случае Н-волн имеется только поперечная составляющая электрического поля. Устремив длину волны к критической, получим наличие продольной составляющей магнитного поля, относительно поперечных пластин эти составляющие ориентированы перпендикулярно, а поперечные составляющие электрического поля тангенциально.

Колебание E_mnо возможно, при этом резонансные явления наблюдаются в поперечной плоскости. В продольном направлении резонансные явления отсутствуют.

Колебания H_mnо – невозможны.