2. Виды и методы измерений

Вид измерений – часть области измерений, имеющая свои особенности и отличающаяся однородностью измеряемых величин. Например, в области электрических и магнитных измерений могут быть выделены как виды измерений: электрического сопротивления, электродвижущей силы, электрического напряжения, магнитной индукции и др.

Метод измерений – часть области измерений, состоящая в различии приемов использования принципов и средств измерений.

Принцип измерений – положенное в основу измерений физическое явление или эффект. Например: эффекты Джозефсона для измерения электрического напряжения, Пельтье для измерения поглощенной энергии ионизирующих излучений, Доплера для измерения скорости.

1. Классификация видов измерений

Классификацию видов измерений можно проводить по различным классификационным признакам, к которым можно отнести следующие: способ нахождения численного значения физической величины, число наблюдений, характер зависимости измеряемой величины от времени, число измеряемых мгновенных значений в заданном интервале времени, условия, определяющие точность результатов, способ выражения результатов измерения (рисунок 2.1).

По способу нахождения численного значения физической величины измерения подразделяются на прямые, косвенные, совокупные и совместные.

Прямым измерением называют измерение, при котором значение измеряемой физической величины получают непосредственно. К ним относятся нахождение физической величины по шкале прибора, например, измерение длины детали микрометром; измерение силы тока микроамперметром. Прямые измерения характеризуются тем, что они выполняются при помощи средств, предназначенных для измерения данных величин. Числовое значение измеряемой величины считывается непосредственно по показанию измерительного прибора.

Зависимость между результатом измерения и измеряемой величиной при прямом измерении характеризуется уравнением , т. е. значение измеряемой величины принимается равным полученному результату.

Прямое измерение не всегда можно выполнить. В таких случаях эффективно использовать косвенное измерение.

Косвенными измерениями называют такие измерения, при которых искомое значение физической величины находят на основании результатов прямых измерений других физических величин, функционально связанных с искомой величиной. Числовое значение искомой величины находят вычислением по формуле

, (2.1)

где – значения непосредственно измеряемых величин.

Примером косвенного измерения является определение электрического сопротивления с помощью амперметра и вольтметра. Здесь путем прямых измерений находят значения падения напряжения на сопротивлении и ток через него, а искомое сопротивление находят по формуле

.

Плотность материала детали, например в виде цилиндра, можно измерить только косвенно: по результатам прямых измерений его массы , высоты и диаметра , связанных с плотностью соотношением

.

Операцию вычисления измеряемой величины можно производить вручную или с помощью вычислительного устройства, помещенного в прибор.

Прямые и косвенные измерения в настоящее время широко используются на практике и являются наиболее распространенными видами измерений.

Совокупные измерения – производимые одновременно измерения нескольких одноименных величин, при которых искомые значения величин определяют путем решения системы уравнений, получаемых при измерениях этих величин в различных сочетаниях.

Для определения значений искомых величин число уравнений должно быть не меньше числа этих величин. Примером совокупных измерений является нахождение сопротивления двух резисторов по результатам измерения сопротивлений при их последовательном и параллельном включении.

Более сложный пример определения значений сопротивлений резисторов, соединенных по схеме треугольника (рисунок 2.2). Здесь измеряют сопротивления между каждой парой вершин треугольника и получают систему уравнений

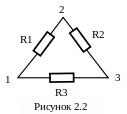
Из решения этой системы уравнений получают значения сопротивлений

;

;

,

где .

Совокупные измерения – проводимые одновременно измерения нескольких одноименных величин, при которых искомые значения величин определяют путем решения системы уравнений, получаемых при измерениях этих величин в различных сочетаниях. Например, значения массы определенных гирь набора определяют по известному значению массы одной из гирь и по результатам сравнений (измерений) масс различных сочетаний гирь.

Совместные измерения – проводимые одновременно измерения двух или нескольких неодноименных величин , для определения зависимости между ними. Значения искомых величин находят решением системы уравнений:

,

где

– результаты прямых или косвенных измерений.

Например, индуктивность катушки , где – индуктивность при частоте , стремящейся к нулю; – межвитковая емкость. Значения и нельзя найти прямыми или косвенными измерениями. Поэтому в простейшем случае измеряют при , а затем при и составляют систему уравнений:

решая которую находят искомые значения индуктивности и емкости :

Совокупные и совместные измерения есть обобщение косвенных измерений на случай нескольких величин.

Для повышения точности совокупных и совместных измерений необходимо выполнить условия , т. е. число уравнений должно быть больше или равно числу искомых величин. Получающуюся при этом несовместную систему уравнений решают методом наименьших квадратов.

По числу измерений последние подразделяются на (рисунок 2.1):

– однократное – выполненное один раз;

– многократное – измерение физической величины одного и того же размера, результат которого получен из нескольких следующих друг за другом измерений, т. е. состоящее из ряда однократных измерений.

По характеру зависимости измеряемой величины от времени измерения разделяются:

– на статические, при которых измеряемую величину принимают в соответствии с конкретной измерительной задачей за неизменную на протяжении времени измерения;

– динамические, при которых измеряемая величина изменяется по размеру в процессе измерения.

Например, измерение длины детали при нормальной температуре – статическое измерение, измерение электрического напряжения в тяговой сети – динамическое. Термин «динамическое» относится к измеряемой величине. Однако, очевидно, что для оценки точности результатов динамических измерений необходимо знание динамических свойств средств измерений.

Строго говоря, все физические величины подвержены тем или иным изменениям во времени. В этом убеждает применение все более и более чувствительных средств измерений, которые дают возможность обнаруживать изменение величин, ранее считавшихся постоянными, поэтому разделение измерений на динамические и статические является условным.

По числу измеряемых мгновенных значений в заданном интервале времени измерения подразделяются на дискретные и непрерывные (аналоговые).

Дискретные измерения – измерения, при которых на заданном интервале времени число измеряемых мгновенных значений конечно.

Непрерывные (аналоговые) измерения – измерения, при которых на заданном интервале времени число измеряемых мгновенных значений бесконечно.

По условиям, определяющим точность результатов, измерения бывают равноточные и неравноточные.

Равноточные измерения – ряд измерений какой-либо величины, выполненных одинаковыми по точности средствами измерений в одних и тех же условиях с одинаковой тщательностью.

Неравноточные измерения – ряд измерений какой-либо величины, выполненных различающимися по точности средствами измерений и (или) в разных условиях. Ряд неравноточных измерений обрабатывают с учетом веса отдельных измерений.

Здесь уместно пояснить следующие термины. Ряд измерений (результатов измерений) – значения одной и той же величины, полученные из следующих друг за другом измерений. Среднее значение из ряда неравноточных измерений определяется с учетом веса каждого единичного измерения. Среднее взвешенное значение иногда называют средним весовым. Вес измерения – это положительное число « », служащее оценкой доверия к тому или иному отдельному результату измерения, входящему в ряд неравноточных измерений. В большинстве случаев принято считать, что веса входящих в ряд неравноточных измерений обратно пропорциональны квадратам их средних квадратических погрешностей, т. е.

.

Для простоты обычно результату с большей погрешностью приписывают вес, равный , а остальные веса находят по отношению к нему.

По способу выражения результатов измерения различают абсолютные и относительные измерения.

Абсолютные измерения – измерения, основанные на прямых измерениях одной или нескольких основных величин и (или) использовании значений физических констант.

Относительные измерения – измерения отношения величины к одноименной величине, играющей роль единицы, или измерения изменения величины по отношению к одноименной величине, принимаемой за исходную.

Например, измерение силы – абсолютное измерение, т. к. оно основано на измерении основной величины – массы « » в точке измерения массы.

Понятие «абсолютное измерение» применяется как противоположное понятию «относительное измерение» и рассматривается как измерение величины в ее единицах. В таком понимании это понятие находит все большее и большее применение.