Работу выполнил студент группы зТс-41

Кузьменко Ю.Г.

Лабораторная работа № 3 Построение регрессионной модели системы двух случайных величин

Цель работы: ознакомиться с основными понятиями регрессионного и корреляционного анализа; исследовать зависимость между двумя случайными величинами, заданными выборками.

Задание: по виду корреляционного поля сделать предположение о форме регрессионной зависимости между двумя случайными величинами; используя метод наименьших квадратов, найти параметры уравнения регрессии; оценить качество описания зависимости полученным уравнением регрессии.

По результатам тридцати совместных измерений веса грузового поезда Х, т, и соответствующего времени технического обслуживания состава Y, мин, представленных в двух первых столбцах таблицы 1, следует исследовать зависимость между данными величинами. Необходимо определить коэффициенты уравнения регрессии методом наименьших квадратов, оценить тесноту связи между величинами, проверить значимость коэффициента корреляции.

1. На величину времени технического обслуживания состава Y, помимо веса X, влияние оказывает ряд других факторов. Поэтому зависимость между величиной времени технического обслуживания состава Y и веса поезда X является статистической: при одном весе поезда при различных дополнительных условиях время технического обслуживания состава может принимать различные значения.

2. Для определения вида регрессионной зависимости построим корреляционное поле.

Рис.1. Корреляционное поле

Характер расположения точек на диаграмме рассеяния позволяет сделать предположение о линейной регрессионной зависимости между величинами Х и Y: .

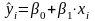Таблица 1 - Результаты промежуточных вычислений

	Вес грузового состава, т,	Время технического обслуживания состава, мин,
1	4435,68	70,9	-463,38	214722,26	1,08	1,16	-498,91
2	5100,58	75,9	201,52	40609,77	6,08	36,93	1224,56
3	4885,41	75,9	-13,65	186,36	6,08	36,93	-82,95
4	5416,94	66,2	517,88	268198,31	-3,62	13,13	-1876,45
5	4496,66	61,9	-402,40	161926,83	-7,92	62,78	3188,36
6	4722,08	63,8	-176,98	31322,39	-6,02	36,28	1066,02
7	5537,91	78,4	638,85	408127,62	8,58	73,56	5479,19
8	5074,01	76,6	174,95	30607,04	6,78	45,92	1185,57
9	4807,09	65,6	-91,97	8458,73	-4,22	17,84	388,43
10	4046,02	72	-853,04	727679,52	2,18	4,74	-1856,79
11	4683,93	68,5	-215,13	46281,49	-1,32	1,75	284,69
12	4872,42	65,4	-26,64	709,76	-4,42	19,57	117,84
13	4003,22	74,7	-895,84	802531,69	4,88	23,78	-4368,72
14	4628,01	63,4	-271,05	73468,83	-6,42	41,26	1741,05
15	4293,44	61,9	-605,62	366777,20	-7,92	62,78	4798,54
Итого	71003,4	1041,1	0,00	2770747,429	0,00	475,79	9756,05
Среднее	4733,56	69,41

3. Вычислим коэффициенты эмпирического уравнения линейной регрессии методом наименьших квадратов .

Средний вес грузового состава:

= т.

Среднее значение времени технического обслуживания состава:

= мин.

Коэффициенты уравнения:

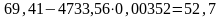
Таким образом, эмпирическое уравнение регрессии имеет вид : .

Изобразим на корреляционном поле линию регрессии:

Рис.2. Корреляционное поле и линия регрессии

4. Вычислим значение эмпирического коэффициента корреляции:

= .

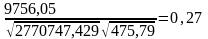Коэффициент корреляции характеризует тесноту связи между двумя случайными величинами в случае наличия между ними линейной зависимости. Т.к. = 0,27, то можно говорить о том, что между величинами X и Y связь не значительная.

Чтобы сделать статистический вывод о значимости эмпирического коэффициента корреляции выдвигается нулевая гипотеза об отсутствии линейной зависимости между исследуемыми случайными величинами против альтернативной гипотезы о наличии линейной связи:

,

.

Если гипотеза H₀ отклоняется, то считается, что между величинами X и Y имеет место зависимость линейного вида.

Для проверки гипотезы H₀ вычисляется t-статистика

= .

При условии справедливости гипотезы H₀ рассчитанная t-статистика имеет распределение Стьюдента с n – 2 степенями свободы. Найденное значение t =1,006 сравнивается с критическим значением t_, при  = n – 2 = 30-2 = 28 степенях свободы. В нашем случае t_, = t _{=0.05, =28} = 1,701. Так как расчетное значение 1,006 по абсолютной величине меньше табличного значения 1,701 для заданного уровня значимости a=0.05, то нет оснований для отклонения нулевой гипотез H₀ о линейной независимости двух случайных величин.