
- •Лабораторная работа № 1 первичная обработка статистических данных
- •Работу выполнил студент группы зТс-41
- •Лабораторная работа № 2 подбор закона распределения одномерной случайной величины
- •Работу выполнил студент группы зТс-41
- •Лабораторная работа № 3 Построение регрессионной модели системы двух случайных величин
- •Работу выполнил студент группы зТс-41
Лабораторная работа № 1 первичная обработка статистических данных
Цель работы: Ознакомится с основными понятиями математической статистики и методикой проведения первичного исследования статистических данных.
Задание: произвести первичную обработку полученных экспериментальных данных и сделать обоснованный вывод о свойствах изучаемой случайной величины.
1. При проведении экспериментов фиксировались значения случайной величины X, характеризующей время технического обслуживания подвижного состава (в минутах). (Значения выборки записаны во втором столбце таблицы 1).
2. Составим расчетную таблицу, в которой запишем вариационный ряд (элементы выборки в порядке возрастания) и произведем расчеты, необходимые для вычисления оценок числовых характеристик.
Таблица 1 – Расчетная таблица
Номер п/п |
Выборка, мин. |
Вариационный ряд, мин. |
|
|
|
|
1 |
70,9 |
60 |
-10,278 |
105,637 |
-1085,740 |
11159,236 |
2 |
75,9 |
60,3 |
-9,978 |
99,560 |
-993,415 |
9912,290 |
3 |
75,9 |
60,5 |
-9,778 |
95,609 |
-934,868 |
9141,135 |
4 |
66,2 |
60,8 |
-9,478 |
89,832 |
-851,432 |
8069,875 |
5 |
61,9 |
61,9 |
-8,378 |
70,191 |
-588,059 |
4926,760 |
6 |
63,8 |
61,9 |
-8,378 |
70,191 |
-588,059 |
4926,760 |
7 |
78,4 |
62 |
-8,278 |
68,525 |
-567,252 |
4695,715 |
8 |
76,6 |
62,300 |
-7,978 |
63,648 |
-507,788 |
4051,130 |
9 |
65,6 |
63,1 |
-7,178 |
51,524 |
-369,837 |
2654,690 |
10 |
72 |
63,4 |
-6,878 |
47,307 |
-325,377 |
2237,941 |
11 |
68,5 |
63,8 |
-6,478 |
41,964 |
-271,846 |
1761,018 |
12 |
65,4 |
63,8 |
-6,478 |
41,964 |
-271,846 |
1761,018 |
13 |
74,7 |
64,6 |
-5,678 |
32,240 |
-183,057 |
1039,397 |
14 |
63,4 |
65,4 |
-4,878 |
23,795 |
-116,071 |
566,197 |
15 |
61,9 |
65,6 |
-4,678 |
21,884 |
-102,372 |
478,896 |
16 |
76,2 |
65,8 |
-4,478 |
20,052 |
-89,795 |
402,102 |
17 |
77,6 |
66,100 |
-4,178 |
17,456 |
-72,930 |
304,701 |
18 |
72,7 |
66,1 |
-4,178 |
17,456 |
-72,930 |
304,701 |
19 |
66,8 |
66,2 |
-4,078 |
16,630 |
-67,817 |
276,560 |
20 |
62,3 |
66,8 |
-3,478 |
12,096 |
-42,072 |
146,325 |
21 |
63,1 |
68 |
-2,278 |
5,189 |
-11,821 |
26,929 |
22 |
70,1 |
68,5 |
-1,778 |
3,161 |
-5,621 |
9,994 |
23 |
75,5 |
68,8 |
-1,478 |
2,184 |
-3,229 |
4,772 |
24 |
66,1 |
69,4 |
-0,878 |
0,771 |
-0,677 |
0,594 |
25 |
69,4 |
70,100 |
-0,178 |
0,032 |
-0,006 |
0,001 |
26 |
71,2 |
70,9 |
0,622 |
0,387 |
0,241 |
0,150 |
27 |
65,8 |
71,2 |
0,922 |
0,850 |
0,784 |
0,723 |
28 |
79 |
71,6 |
1,322 |
1,748 |
2,310 |
3,054 |
29 |
60,5 |
72 |
1,722 |
2,965 |
5,106 |
8,793 |
30 |
77,3 |
72,6 |
2,322 |
5,392 |
12,519 |
29,070 |
31 |
78,1 |
72,7 |
2,422 |
5,866 |
14,208 |
34,411 |
32 |
60,8 |
74,7 |
4,422 |
19,554 |
86,468 |
382,362 |
33 |
78,9 |
75,5 |
5,222 |
27,269 |
142,400 |
743,614 |
34 |
64,6 |
75,8 |
5,522 |
30,492 |
168,379 |
929,792 |
35 |
62 |
75,9 |
5,622 |
31,607 |
177,694 |
998,995 |
36 |
63,8 |
75,9 |
5,622 |
31,607 |
177,694 |
998,995 |
37 |
72,6 |
76,200 |
5,922 |
35,070 |
207,685 |
1229,911 |
38 |
66,1 |
76,5 |
6,222 |
38,713 |
240,874 |
1498,718 |
39 |
77,7 |
76,6 |
6,322 |
39,968 |
252,676 |
1597,416 |
40 |
68 |
76,7 |
6,422 |
41,242 |
264,857 |
1700,909 |
41 |
76,7 |
77,3 |
7,022 |
49,308 |
346,244 |
2431,327 |
42 |
60,3 |
77,600 |
7,322 |
53,612 |
392,545 |
2874,213 |
43 |
78,5 |
77,7 |
7,422 |
55,086 |
408,849 |
3034,477 |
44 |
78,8 |
78,1 |
7,822 |
61,184 |
478,579 |
3743,443 |
45 |
76,5 |
78,4 |
8,122 |
65,967 |
535,783 |
4351,630 |
46 |
60 |
78,5 |
8,222 |
67,601 |
555,818 |
4569,934 |
47 |
68,8 |
78,8 |
8,522 |
72,624 |
618,906 |
5274,316 |
48 |
75,8 |
78,9 |
8,622 |
74,339 |
640,950 |
5526,270 |
49 |
71,6 |
79 |
8,722 |
76,073 |
663,511 |
5787,145 |
50 |
79,6 |
79,6 |
9,322 |
86,900 |
810,079 |
7551,555 |
Итого |
3513,9 |
3513,9 |
0,0000000000004 |
1994,326 |
-918,757 |
124159,956 |
Найдем
размах выборки
 = 79,6 – 60,0 = 19,6
= 79,6 – 60,0 = 19,6
Длина
интервала
 =
= =
= = 2,950
= 2,950
4) границы интервалов:
 =
60,0,
=
60,0,
 =
60,0 + 2,995 = 62,950,
=
60,0 + 2,995 = 62,950,
 =
62,995 + 2,995 = 65,900,
=
62,995 + 2,995 = 65,900,
 =
65,990 + 2,995 = 68,850,
=
65,990 + 2,995 = 68,850,
 =
68,985 + 2,995 = 71,800,
=
68,985 + 2,995 = 71,800,
 =
71,980 + 2,995 = 74,750,
=
71,980 + 2,995 = 74,750,
 =
74,975 + 2,995 = 77,700
=
74,975 + 2,995 = 77,700
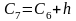 =
77,970+ 2,995 = 80,650
=
77,970+ 2,995 = 80,650
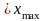 .
.
3. Построим интервальный статистический ряд (Таблица 2).
Таблица 2 – Интервальный статистический ряд
Г |
Ч |
Ч |
Накопленные частости |
, мин. |
|||
60 |
8
|
0,160
|
0,160
|
62,950 |
|||
62,950 |
8
|
0,16
|
0,32
|
65,900 |
|||
65,900 |
7
|
0,140
|
0,460
|
68,850 |
|||
68,850 |
5
|
0,100
|
0,560
|
71,800 |
|||
71,800 |
4
|
0,080
|
0,640
|
74,750 |
|||
74,750 |
11
|
0,220
|
0,860
|
77,700 |
|||
77,700 |
7
|
0,140
|
1,000
|
80,650 |
|||
Итого |
50 |
1 |
|
Гистограмма относительных частот приведена на рис. 1

Рисунок 1 – Гистограмма относительных частот
4. Вычислим точечные оценки числовых характеристик.
В
качестве оценки математического
ожидания
используется среднее арифметическое
 выборочных значений. Эта статистика
называется выборочным
средним.
выборочных значений. Эта статистика
называется выборочным
средним.
 .
.
Для
оценивания по выборочным данным моды
распределения, используется то значение
сгруппированного статистического ряда
 ,
которому соответствует наибольшее
значение частоты. По интервальному
статистическому ряду определяется
модальный интервал, в который попало
наибольшее
число элементов выборки,
и в качестве точечной оценки моды может
использоваться среднее значение этого
интервала.
,
которому соответствует наибольшее
значение частоты. По интервальному
статистическому ряду определяется
модальный интервал, в который попало
наибольшее
число элементов выборки,
и в качестве точечной оценки моды может
использоваться среднее значение этого
интервала.
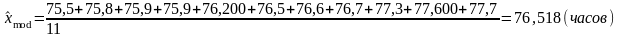 .
.
Для
определения выборочного значения
медианы используется вариационный ряд.
В качестве оценки медианы
 принимают средний (т. е.
принимают средний (т. е.
 -й)
член этого ряда, если значение n –
нечётно и среднее арифметическое между
двумя средними (т. е. между
-й)
член этого ряда, если значение n –
нечётно и среднее арифметическое между
двумя средними (т. е. между
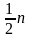 -м
и
-м
и
 -м)
членами этого ряда, если n –
чётно. В нашем случае объем выборки
-м)
членами этого ряда, если n –
чётно. В нашем случае объем выборки
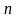 =
50 - четное, т.е. в качестве оценки медианы
примем
=
50 - четное, т.е. в качестве оценки медианы
примем
=
 .
.
В качестве оценки дисперсии используется статистика
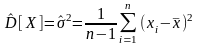 =
=
 .
.
Оценка среднего квадратического отклонения:
 =
=
 .
.
Оценка коэффициента вариации
 .
.
Оценка коэффициента асимметрии
 .
.
Оценка коэффициента эксцесса
 .
.
Построим
интервальные оценки для неизвестных
истинных значений
 и
и
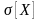 .
.
Объем
выборки составил n
= 50. Требуется с доверительной вероятностью
 определить интервальные оценки:
определить интервальные оценки:
а) для среднего времени технического обслуживания подвижного состава;
б) для дисперсии времени технического обслуживания подвижного состава;
в) для среднего квадратичного отклонения времени технического обслуживания подвижного состава
а)
Средняя стоимость времени технического
обслуживания подвижного состава
характеризуется генеральной средней
a.
Требуется найти интервальную оценку
 параметра a
с доверительной вероятностью
.
параметра a
с доверительной вероятностью
.
Применяем формулу
 ,
,
где
 ,
,
 ,
,
 ,
,
 ,
значение
,
значение
 определяем по таблицам распределения
Стьюдента для
определяем по таблицам распределения
Стьюдента для
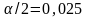 и
.
и
.
 .
Подставим найденные значения в формулу:
.
Подставим найденные значения в формулу:

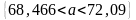 мин
мин
Таким образом, с вероятностью можно гарантировать, что среднее время технического обслуживания подвижного состава:
 .
.
б) определим интервальную оценку для дисперсии стоимости строительно-монтажных работ на участке.
Интервальная оценка дисперсии
 .
.
По
таблице процентных точек
 -распределения
(см. приложение Г) найдем
-распределения
(см. приложение Г) найдем
 ;
;
 .
.
Следовательно,
 .
.
Значит с доверительной вероятностью можно утверждать, что истинное значение дисперсии будет находиться в интервале

в) С доверительной вероятностью можно утверждать, что истинное значение среднего квадратичного отклонения будет находиться в интервале

7) Произведем первичную обработку полученной выборки с помощью ЭВМ:
Summary Statistics for Col_1
Count |
50 |
Average |
70,278 |
Median |
70,5 |
Mode |
76,518 |
Variance |
40,7005 |
Standard deviation |
6,3797 |
Coeff. of variation |
9,0778% |
Minimum |
60,0 |
Maximum |
79,6 |
Range |
19,6 |
Skewness |
-0,07522 |
Kurtosis |
-1,46385 |
Sum |
3513,9 |


Рисунок 1.4 – Компьютерный расчет
Confidence Intervals for X
95,0% confidence interval for mean: 70,278 +/- 1,81309 [68,4649; 72,0911]
95,0% confidence interval for standard deviation: [5,32918; 7,94995]
The StatAdvisor
This pane displays 95,0% confidence intervals for the mean and standard deviation of X. The classical interpretation of these intervals is that, in repeated sampling, these intervals will contain the true mean or standard deviation of the population from which the data come 95,0% of the time. In practical terms, we can state with 95,0% confidence that the true mean X is somewhere between 68,4649 and 72,0911, while the true standard deviation is somewhere between 5,32918 and 7,94995.
.
Вывод. В результате исследования выборки значений непрерывной случайной величины, характеризующей время технического обслуживания подвижного состава, получили следующие результаты, минут: минимальное время технического обслуживания подвижного состава – 60,0, максимальное – 79,6, среднее значение времени технического обслуживания подвижного состава – 70,258, наиболее вероятное время технического обслуживания подвижного состава – 76,518, средневероятное – 70,5, среднеквадратическое отклонение времени технического обслуживания подвижного состава от среднего значения составило 6,380. С доверительной вероятностью можно гарантировать, что среднее время обслуживания подвижного состава находится в пределах: , истинное значение дисперсии будет находиться в интервале , истинное значение среднего квадратичного отклонения будет находиться в интервале
