3. Математична модель

При розробці і дослідженні систем автоматизованого управління ядерними енергетичними установки (ЯЕУ) користуються математичним моделюванням. Враховуючи всі складні динамічні процеси, для сучасних 2-контурних ЯЕУ з реакторами типу ВВЕР математична модель (ММ) описується системою багатьох нелінійних диференціальних рівнянь. Дослідження такої системи ускладнене. Водночас для деяких інженерних і навчальних завдань можливе використання спрощених ММ, які забезпечують достатню точність [4].

1. Виведення рівнянь динаміки енергоблоку

   1. Розрахункова схема

На рис. 3.1 зображена принципова схема 2-контурної АЕС з реактором 1, парогенератором (ПГ) 2, турбіною 3 и циркуляційними насосами 4 и 5 з позначенням фізичних величин: – температура теплоносія на вході в реактор; – температура теплоносія на виході з реактора; – температура теплоносія на вході в ПГ; – температура теплоносія на виході з ПГ; – паропродуктивність; – температура насиченої пари; – ентальпія підживлювальної води.

Рис. 3.1 – Технологічна схема 2-контурної АЕС

Ядерний реактор описується рівняннями кінетики, які зв'язують реактивність ρ з відносною густиною нейтронів n, і рівнянням температурного ефекту реактивності по теплоносію та паливу. Крім того, в ЯЕУ включені наступні структурні елементи (рис. 3.2): 1 – ядерний реактор; 2 – ядерне паливо; 3 – оболонка тепловиділяючого елемента; 4 – теплоносій в реакторі; 5 – трубопроводи до реактора і ПГ; 6 – трубопроводи від реактора і ПГ; 7 – ПГ по теплоносію першого контуру; 8 – ПГ по теплоносію другого контуру. Фізичні величини: – температура палива; – температура оболонки; 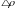– зміна реактивності; – зовнішня реактивність.

Рис. 3.2 – Структурна схема енергоблоку АЕС

2. Виведення рівнянь динаміки елементів структурної схеми

Кінетика ядерного реактора описується системою з 7 диференціальних рівнянь, які враховують 6 груп запізнілих нейтронів.

З урахуванням однієї групи запізнілих нейтронів, а також з урахуванням нехтування часом життя нейтронів, рівняння кінетики можна представити наступного вигляду (елемент 1):

, (3.1)

де – приріст густини нейтронів;

– густина нейтронів в сталому стані;

– реактивність;

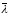– середнє значення постійної розпаду;

– частка запізнілих нейтронів.

Для відносної густини нейтронів маємо:

(3.2)

Для малих відхилень нейтронного потоку від стаціонарного значення зв'язок між теплоносієм і нейтронним потоком визначається виразом (3.3):

(3.3)

Температурний коефіцієнт реактивності враховується рівнянням (елемент 9):

, (3.4)

де – коефіцієнт реактивності по теплоносію;

– середня температура теплоносія 1-го контуру;

– коефіцієнт реактивності по паливу;

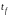– температура палива.

При розгляді інших елементів ЯЕУ приймемо такі припущення: всі елементи являють собою об'єкти із зосередженими параметрами, тепловими втратами в навколишнє середовище нехтуємо.

Рівняння збереження енергії для палива (елемент 2):

, (3.5)

де – теплова потужність реактора;

– загальна довжина тепловиділяючих елементів (ТВЕЛ);

– термічний опір палива на одиницю довжини ТВЕЛа;

– середня температура палива;

– температура оболонки;

– питома теплоємність палива;

– маса палива;

Для розв’язку (3.5), а також подальших рівнянь необхідно знати , і т.д.

Однак для отримання спрощеної моделі для діючих ЯЕУ можна не володіти подібними відомостями про параметри ЯЕУ і вчинити так.

Для стаціонарного режиму:

, тоді (3.6)

Температури , відомі для стаціонарного режиму, тому комплекс можна визначити.

Позначимо

(3.7)

Тоді рівняння (3.5) можна записати:

(3.8)

Представимо рівняння у вигляді вихідної координати:

(3.9)

Рівняння передачі теплоти через оболонку ТВЕЛа (елемент 3):

, (3.10)

де 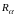– термічний опір теплопередачі в каналі;

– поверхня оболонок;

– середня температура теплоносія;

– питома теплоємність матеріалу і маса оболонки.

Середня температура теплоносія розраховується за формулою (3.11):

, (3.11)

де – температура теплоносія на вході в реактивну зону;

– температура теплоносія на виході із реактивної зони.

В стаціонарному стані , тоді

(3.12)

Позначимо

(3.13)

Звідси (3.10) можна записати так:

(3.14)

Рівняння теплового балансу для теплоносія (елемент 4):

, (3.15)

де – питома теплоємність теплоносія;

– витрата теплоносія;

– обсяг теплоносія в активній зоні реактора;

– питома теплоємність металу реакторного корпусу;

– густина теплоносія першого контуру;

– маса корпусу реактора і його внутрішньокорпусних пристроїв.

Для стаціонарного стану , тоді

(3.16)

Позначимо

(3.17)

З урахуванням введення коефіцієнтів рівняння (3.15) запишеться так:

(3.18)

(3.19)

Представимо через , :

(3.20)

Зважаючи на кінцеву швидкість теплоносія, необхідно врахувати запізнювання передачі теплоти на ділянці від реактора до парогенератора і назад (елемент 5 і 6).

Це запізнювання представимо експонентною залежністю:

, (3.21)

, (3.22)

де і – температура теплоносія на вході і виході парогенератора

відповідно.

Коефіцієнти 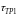і визначаються через довжину трубопроводів і швидкість теплоносія :

(3.23)

, (3.24)

де і – довжина трубопроводу від реактора до ПГ і від ПГ до реактора

відповідно.

і – довжина трубопроводу від реактора до ПГ і від ПГ до реактора

відповідно.

Оскільки втратами теплоти в навколишнє середовище нехтуємо, то для стаціонарного режиму

і (3.25)

Перепишемо рівняння (3.21) і (3.22):

, (3.26)

(3.27)

Рівняння теплового балансу ПГ з боку теплоносія першого контуру (елемент 7):

, (3.28)

де – поверхня нагріву ПГ;

– термічний опір теплопередачі в ПГ;

– обсяг теплоносія 1-го контуру;

– питома теплоємність матеріалу ПГ;

– маса матеріалу трубної системи ПГ, що бере участь в акумуляції

теплоти від теплоносія першого контуру;

– температура насиченої пари.

Для стаціонарного режиму , тоді

(3.29)

Позначимо

(3.30)

З урахуванням введення позначень

(3.31)

Рівняння теплового балансу ПГ з боку теплоносія 2-го контуру (елемент 8):

, (3.32)

де – ентальпія сухої насиченої пари;

– питома теплоємність теплоносія 2-го контуру;

– обсяг теплоносія 2-го контуру;

– густина теплоносія 2-го контуру;

– паропродуктивність;

– ентальпія підживлювальної води;

– маса ПГ без трубної системи.

Для стаціонарного режиму , тоді

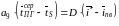, (3.33)

звідки

, (3.34)

Позначимо

(3.35)

Ентальпія функціонально пов'язана з температурою насичення , тобто . При малому відхиленні параметрів від усталеного стану цю залежність можна представити (40):

, (3.36)

де – коефіцієнти, які визначаються аналітично для конкретних

параметрів пари.

Підставимо (3.36) в (3.32):

, (3.37)

(3.38)

Останнє рівняння є нелінійним, оскільки містить похідні змінних і .

Лінеаризуємо його, записавши змінні в відхиленнях:

(3.39)

де і – значення змінних в сталому стані.

Рівняння (3.2), (3.4), (3.9), (3.14), (3.20), (3.26), (3.27), (3.31), (3.39) складають систему рівнянь енергоблоку.

При записі наступних рівнянь зробимо такі перетворення:

• рівняння (3.2) проінтегруємо з урахуванням нульових початкових умов;

• всі рівняння системи запишемо у відхиленнях;

• рівняння (3.9) запишемо з урахуванням (3.3);

• середні температури в реакторі і ПГ виразимо через відповідні вхідні і вихідні температури.

Доповнимо отриману систему рівнянням суматора для реактивності:

(3.40)

де – реактивність, яка вноситься з боку (зовнішня) (див. рис. 3.2).

Тоді отримаємо таку систему рівнянь:

(3.41)

В системі (3.41) були прийняті наступні позначення:

(3.42) (3.52)

(3.43) (3.53)

(3.44) (3.54)

(3.45) (3.55)

(3.46) (3.56)

(3.47) (3.57)

(3.48) (3.58)

(3.49) (3.59)

(3.50) (3.60)

(3.51) (3.61)

Вихідними величинами в системі (3.41) є:

• відносна потужність реактора ;

• температура палива ;

• температура оболонки ;

• температура теплоносія на вході і на виході реактора;

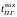• температура теплоносія на вході парогенератора і виході . Вихідними збуреннями є:

• зовнішня реактивність ;

• витрата пара .