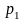Курсовая работа по теме ««Исследование надежности систем»»
Задание
1. Найти
надежность системы, состоящей из 5
независимых элементов с надежностями:
.
На рисунке (см.
Приложение №1) представлена система из
пяти независимо работающих элементов.
Обозначим
событие, состоящее в том, что элемент
«
»
работает. Используя операции алгебры
событий, выразить событие
состоящее
в том, что система из пяти элементов
работает, через события
.
Задание
2. В системе
m исправных
элементов и n
неисправных. Случайным образом проверяют
2 элемента. Какова вероятность того, что
проверенные элементы:
а) оба исправны; б) оба не исправны; в) один исправен, а второй – не исправен?
Вариант |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
m |
5 |
4 |
3 |
6 |
7 |
5 |
8 |
4 |
6 |
7 |
5 |
4 |
3 |
6 |
7 |
n |
3 |
2 |
7 |
3 |
2 |
4 |
3 |
7 |
4 |
4 |
3 |
2 |
7 |
3 |
2 |
Вариант |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
30 |
m |
5 |
4 |
3 |
6 |
7 |
5 |
8 |
4 |
6 |
7 |
5 |
4 |
3 |
6 |
7 |
n |
3 |
2 |
7 |
3 |
2 |
4 |
3 |
7 |
4 |
4 |
3 |
2 |
7 |
3 |
2 |
Задание 3. Производительность первого конвейера в k раз больше, чем второго. Первый конвейер допускает p% брака, второй q% , брака. Детали с обоих конвейеров поступают на склад.
а) Какова вероятность того, что случайно взятая со склада деталь будет стандартна?
б) Какова вероятность того, что случайно взятая со склада деталь будет не стандартна?
в) Случайно выбранная на складе деталь оказалась стандартной. Какова вероятность того, что деталь изготовлена на первом конвейере, на втором конвейере?
Вариант
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
k |
2 |
2.5 |
3 |
3.5 |
4 |
2 |
2.5 |
3 |
3.5 |
4 |
p |
10% |
5% |
15% |
10% |
5% |
15% |
10% |
5% |
15% |
10% |
q |
10% |
10% |
15% |
15% |
5% |
15% |
5% |
10% |
5% |
5% |
Вариант |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
k |
4.5 |
5 |
4.5 |
4 |
3.5 |
3 |
2.5 |
2 |
1.5 |
2 |
p |
10% |
5% |
15% |
10% |
5% |
15% |
10% |
5% |
15% |
10% |
q |
10% |
10% |
15% |
15% |
5% |
15% |
5% |
10% |
5% |
5% |
Вариант |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
30 |
k |
5.5 |
2.5 |
3 |
3.5 |
4 |
2 |
2.5 |
3 |
3.5 |
4 |
p |
10% |
15% |
5% |
5% |
15% |
5% |
10% |
15% |
5% |
10% |
q |
10% |
10% |
15% |
15% |
5% |
15% |
15% |
10% |
5% |
15% |
Задание 4. В первом ящике находится N деталей, из которых M – стандартны. Во втором ящике находится n деталей, из которых m стандартны. Без проверки на стандартность перекладывается из первого ящика во второй k деталей. Какова вероятность того, что случайно взятая из второго ящика деталь будет:
а) стандартна; б) не стандартна?
Вариант |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
N |
100 |
200 |
100 |
200 |
100 |
200 |
100 |
200 |
200 |
100 |
M |
90 |
80 |
80 |
90 |
85 |
85 |
90 |
85 |
90 |
85 |
n |
200 |
100 |
200 |
100 |
200 |
100 |
200 |
100 |
100 |
200 |
m |
80 |
90 |
90 |
80 |
85 |
85 |
85 |
90 |
85 |
90 |
k |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
Вариант |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
N |
100 |
200 |
100 |
200 |
100 |
200 |
100 |
200 |
200 |
100 |
M |
70 |
110 |
75 |
120 |
80 |
125 |
85 |
130 |
90 |
135 |
n |
200 |
100 |
200 |
100 |
200 |
100 |
200 |
100 |
100 |
200 |
m |
80 |
90 |
90 |
80 |
85 |
85 |
85 |
90 |
85 |
90 |
k |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
Вариант |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
30 |
N |
100 |
200 |
100 |
200 |
100 |
200 |
100 |
200 |
200 |
100 |
M |
90 |
80 |
80 |
90 |
85 |
85 |
90 |
85 |
90 |
85 |
n |
200 |
100 |
200 |
100 |
200 |
100 |
200 |
100 |
100 |
200 |
m |
140 |
70 |
135 |
75 |
130 |
80 |
125 |
85 |
95 |
120 |
k |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
Задание
5. Система
состоит из n
элементов с одинаковой вероятностью P
их безотказной работы. Полагая, что
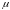– количество исправных элементов, найти
вероятности событий:
=m;
<m;
m;
m1
m2;
m1<
<m2;
1;
<n.
|
Вариант |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
P |
50% |
60% |
70% |
80% |
90% |
50% |
60% |
70% |
80% |
90% |
|
n |
10 |
10 |
10 |
10 |
10 |
10 |
10 |
10 |
10 |
10 |
|
m |
5 |
6 |
7 |
5 |
6 |
7 |
5 |
6 |
7 |
5 |
|
m1 |
3 |
4 |
5 |
3 |
4 |
5 |
3 |
4 |
5 |
3 |
|
m2 |
6 |
7 |
8 |
6 |
7 |
6 |
6 |
7 |
8 |
6 |
|
Вариант |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
|
P |
50% |
60% |
70% |
80% |
90% |
50% |
60% |
70% |
80% |
90% |
|
n |
10 |
10 |
10 |
10 |
10 |
10 |
10 |
10 |
10 |
10 |
|
m |
4 |
5 |
6 |
7 |
8 |
7 |
6 |
5 |
4 |
5 |
|
m1 |
3 |
4 |
5 |
3 |
4 |
5 |
3 |
4 |
5 |
3 |
|
m2 |
6 |
7 |
8 |
6 |
8 |
6 |
6 |
7 |
6 |
6 |
|
Вариант |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
30 |
|
P |
50% |
60% |
70% |
80% |
90% |
50% |
60% |
70% |
80% |
90% |
|
n |
10 |
10 |
10 |
10 |
10 |
10 |
10 |
10 |
10 |
10 |
|
m |
5 |
6 |
7 |
5 |
6 |
7 |
5 |
6 |
7 |
5 |
|
m1 |
3 |
4 |
5 |
3 |
4 |
5 |
3 |
4 |
5 |
3 |
|
m2 |
4 |
5 |
6 |
7 |
8 |
9 |
8 |
7 |
6 |
5 |
Задание
6. Дискретная
случайная величина задана таблицей.
Найти неизвестную вероятность
,
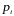математическое ожидание M(X)
и вероятность попадания случайной
величины в интервал
.
Вариант 1,11,21 = –2; = 3 |
|
Вариант 2,12,22 = 2; = 5,8 |
||||||||||||
|
–1 |
0 |
4 |
5 |
6 |
|
–2 |
–1 |
0 |
5 |
6 |
|||
|
0,1 |
0,2 |
|
0,1 |
0,1 |
|
|
0,3 |
0,1 |
0,1 |
0,1 |
|||
Вариант 3,13,23 = 0,2; = 10,7 |
|
Вариант 4,14,24 = –1,12; = 2 |
||||||||||||
|
–3 |
–1 |
0 |
2 |
4 |
|
|
–20 |
0 |
0,5 |
1 |
3 |
||
|
0,1 |
0,3 |
0,1 |
|
0,1 |
|
|
0,1 |
0,1 |
|
0,2 |
0,1 |
||
Вариант 5,15,25 = 1,5; = 10 |
|
Вариант 6,16,26 = 1,3; = 2,7 |
||||||||||||
|
–12 |
0 |
1 |
3 |
4 |
|
|
–5 |
0 |
1 |
2 |
3 |
||
|
0,1 |
0,2 |
0,1 |
0,1 |
|
|
|
|
0,2 |
0,1 |
0,1 |
0,2 |
||
Вариант 7,17,27 = –1,1; = 3 |
|
Вариант 8,18,28 = 1; = 4,2 |
||||||||||||
|
–1 |
–0,5 |
0 |
2 |
7 |
|
|
–2 |
–1 |
0 |
4 |
7 |
||
|
0,1 |
|
0,2 |
0,1 |
0,1 |
|
|
|
0,1 |
0,2 |
0,1 |
0,1 |
||
Вариант 9,19,29 = –10; = –3,5 |
|
Вариант 10,20, 30 = 1,4; = 10,3 |
||||||||||||
|
–5 |
–1 |
0 |
2 |
3 |
|
|
–8 |
–2 |
0 |
1 |
3 |
||
|
0,2 |
|
0,1 |
0,1 |
0,1 |
|
|
0,1 |
0,1 |
0,2 |
0,1 |
|
||
Задание
7. Дана функция
распределения F(x)
случайной
величины X.
Найти плотность распределения вероятности
f(x),
математическое ожидание M(X)
и вероятность попадания случайной
величины в интервал
.
1,11,21 
2.12,22
3,13,23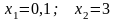 
4,14,24
5,15,25
6,16,26
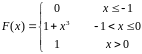
7,17,27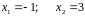 
8,18,28
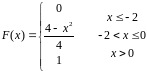
9,19,29 
10,20,30
Задание 8. Дана функция плотности распределения f(x) случайной величины Х. Найти параметр A, функцию распределения F(x), построить графики функций F(x) и f(x), вычислить математическое ожидание МX, дисперсию DX, среднеквадратичное отклонение x, вероятности событий X < x0, X > x0, x1 X x2.