Характерные прямые плоскости – линии уровня и линии наибольшего наклона плоскости

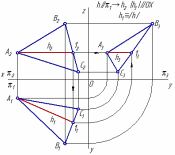
К главным линиям (характерным прямым) плоскости относятся линии уровня и линии наибольшего наклона (рисунок 36).

Р исунок 36 – Классификация главных линий плоскости

Горизонталью h (h₁ и h₂) плоскости называется прямая, лежащая в данной плоскости и параллельная горизонтальной плоскости проекций (рисунок 37). Так как горизонталь плоскости параллельна горизонтальной плоскости проекций П₁, то фронтальная ее проекция будет параллельна оси Х. Для построения проекций горизонтали проводим через точку А₂ прямую, параллельную оси Х. Это будет фронтальная проекция горизонтали (h₂). Горизонтальную проекцию горизонтали (h₁) находим по линии связи.

Рисунок 37 – Горизонталь плоскости

Фронталью плоскости f (f₁ и f₂) называется прямая, лежащая в данной плоскости и параллельная фронтальной плоскости проекций. Горизонтальная проекция фронтали на чертеже параллельна оси Х, а фронтальную проекцию фронтали находим при помощи линии связи (рисунок 38).

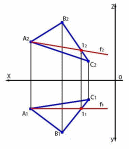Рисунок 38 – Фронталь плоскости

Профильной прямой р (р₁, р₂, р₃) называется прямая линия, принадлежащая плоскости и параллельная профильной плоскости проекций (рисунок 39).

Рисунок 39 – Профильная прямая

В этом случае фронтальная и горизонтальная проекции профильной прямой р (р₁ и р₂) параллельны П₃, а профильная проекция р₃ равняется натуральной величиной.

Линиями наибольшего наклона плоскости к плоскостям проекций (ЛНН) называются линии, проведенные в плоскости и определяющие наибольший угол между плоскостью и плоскостью проекций, т.е. величину образованного двугранного угла. Различают линию наибольшего наклона плоскости к плоскости проекций H (горизонтальная плоскость) – ЛНН(Н), к плоскости проекций V (фронтальная плоскость) – ЛНН(V) и к плоскости проекций W (профильная плоскость) – ЛНН(W). Рассмотрим подробнее первые две линии.

Л иния наибольшего наклона плоскости к плоскости проекций H проводится перпендикулярно к горизонтальному следу плоскости или к горизонтали плоскости. Линия наибольшего наклона плоскости к плоскости проекций V проводится перпендикулярно к фронтальному следу плоскости или к фронтали (рисунок 40).

Рисунок 40 – Построение проекций линий наибольшего наклона

Принцип методики построения проекций ЛНН основывается на теореме прямого угла: если один из катетов прямого угла параллелен какой-либо плоскости, то на эту плоскость прямой угол проецируется в натуральную величину.

1.3.2 Положение плоскости относительно плоскостей проекций (плоскости общего и частного положения). Точка и прямая в плоскости (построение их недостающих проекций)

Положение плоскости относительно плоскостей проекций (плоскости общего и частного положений)

Плоскость в пространстве может занимать относительно плоскостей проекций П₁, П₂, П₃ следующие положения:

– наклонно ко всем плоскостям проекций – плоскость общего положения (рисунок 41);

Рисунок 41 – Плоскость общего положения

– перпендикулярно к одной из плоскостей проекций – проецирующая плоскость;

– перпендикулярно одновременно к двум плоскостям проекций, т.е. параллельно третьей плоскости проекций – плоскость уровня.

Проецирующие плоскости: горизонтально-проецирующая, фронтально-проецирующая, профильно-проецирующая.

П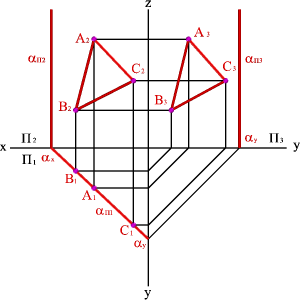 лоскость перпендикулярная горизонтальной плоскости проекций, называется горизонтально проецирующей плоскостью. Горизонтальная проекция такой плоскости представляет собой прямую линию, которая одновременно является её горизонтальным следом. Горизонтальные проекции всех точек любых фигур в этой плоскости совпадают с горизонтальным следом (рисунок 42).

Рисунок 42 – Горизонтально проецирующая плоскость

П лоскость перпендикулярная фронтальной плоскости проекций – фронтально-проецирующая плоскость. Фронтальной проекцией плоскости является прямая линия, совпадающая с фронтальным следом следом (рисунок 43).

Рисунок 43 – Фронтально проецирующая плоскость

П рофильно-проецирующая плоскость – плоскость, перпендикулярная профильной плоскости проекций, задается профильным следом плоскости (рисунок 44).

Рисунок 44 – Профильно-проецирующая плоскость

Плоскости уровня: горизонтальная плоскость – параллельная П₁, фронтальная – параллельная П₂ и профильная – параллельная П₃. Эти плоскости уровня перпендикулярны одновременно двум другим плоскостям проекций.

Горизонтальная плоскость уровня – плоскость, параллельная горизонтальной плоскости проекций и перпендикулярна одновременно фронтальной и профильной плоскостям проекций.

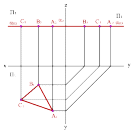Горизонтальная плоскость, заданная треугольником АВС (рисунок 45), изображена проекциями А₁В₁С₁, А₂В₂С₂ и А₃В₃С₃. При этом фронтальная и профильная проекции изображаются отрезками прямых линий, а горизонтальная – треугольником, который равняется истинной величине треугольника АВС, т.к. он в пространстве занимает параллельное положение относительно плоскости проекций П₁.

Рисунок 45 – Горизонтальная плоскость уровня

Фронтальная плоскость уровня – плоскость, параллельная фронтальной плоскости проекций и перпендикулярна одновременно горизонтальной и профильной плоскостям проекций.

Фронтальная плоскость, заданная треугольником АВС (рисунок 46), изображена проекциями А₁В₁С₁, А₂В₂С₂ и А₃В₃С₃. При этом горизонтальная и профильная проекции изображаются отрезками прямых линий, а фронтальная – треугольником, который равняется истинной величине треугольника АВС, т.к. он в пространстве занимает параллельное положение относительно плоскости проекций П_2.

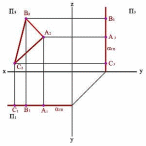Рисунок 46 – Фронтальная плоскость уровня

Профильная плоскость уровня – плоскость, параллельная профильной плоскости проекций и перпендикулярна одновременно горизонтальной и фронтальной плоскостям проекций.

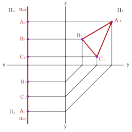Профильная плоскость, заданная треугольником АВС (рисунок 47), изображена проекциями А₁В₁С₁, А₂В₂С₂ и А₃В₃С₃. При этом горизонтальная и фронтальная проекции изображаются отрезками прямых линий, а профильная – треугольником, который равняется истинной величине треугольника АВС, т.к. он в пространстве занимает параллельное положение относительно плоскости проекций П_3.

Рисунок 47 – Профильная плоскость уровня