3. Кинематика жидкости

Основная задача гидромеханики – изучение движущейся жидкости.

Она при этом рассматривается как сплошная среда, без разрывов и пустот. Основными параметрами движения являются давление и скорость. Давление в движущейся жидкости называется гидродинамическим. В идеальной жидкости величина гидродинамического давления в точке, как и у гидростатического, не зависит от направления и является скалярной величиной. В вязкой жидкости из-за влияния касательных напряжений . Однако, в гидромеханике доказывается, что сумма в данной точке постоянна и не зависит от направления; поэтому полагают, что гидродинамическое давление в точке равно среднему из проекций на координатные оси и представляет собой также скалярную величину, то - есть . Если параметры движения − функции только координат точки, то - есть если , движение называется установившимся. Если (p и зависят еще от времени), движение называется неустановившимся. Поскольку жидкость – непрерывная среда, функции p и также непрерывны.

Кинематика изучает законы изменения скорости ; общие же закономерности изменения давления и скорости изучает гидродинамика.

При изучении движущейся жидкости применяются два метода –Лагранжа и Эйлера.

Рис.3.1. Два метода изучения движущейся жидкости:

a − метод Лагранжа; b – метод Эйлера

В методе Лагранжа изучается движение каждой жидкой частицы

(рис. 3.1, а). В момент времени t₀ она находится в точке А с координатами x₀ ,

y₀ , z₀ ; в момент t_k − в точке В с координатами x_k , y_k , z_k . Проекции скорости частицы на координатные оси записываются как

.

Если известны функции , то, проинтегрировав, получим:

; ; .

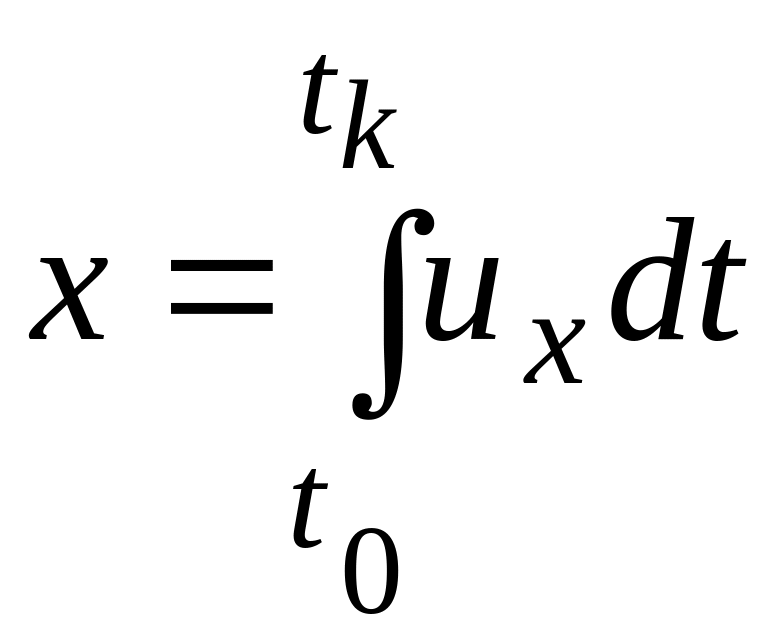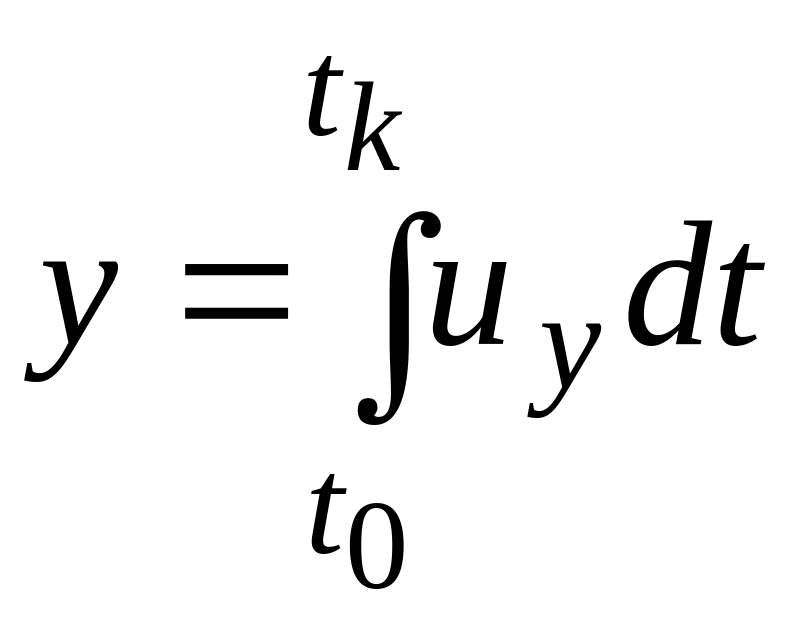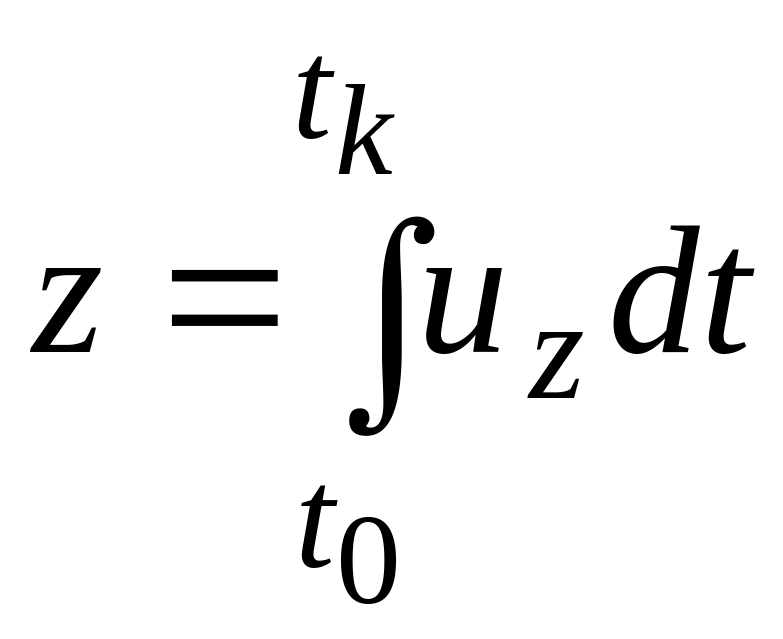Итогом расчета является траектория частицы; она будет зависеть от времени t и начальных координат точки x₀ , y₀ , z₀ .

В методе Эйлера определяются поля скоростей в заданном пространстве, занятом жидкостью (рис. 3.1, b), в данный момент времени, то - есть

; ; .

Метод Эйлера оказывается в большинстве случаев более плодотворным, поэтому он является основным в кинематике и динамике жидкости.

3.1. Основные понятия и определения кинематики жидкости

Линией тока называется линия, проходящая через последовательно движущиеся одна за другой частицы жидкости в данный момент времени.

В каждой точке линии тока вектор скорости касателен к ней ( рис. 3.2, а).

Линия тока и траектория в общем случае − различные кривые и совпадают только при установившемся движении. Поскольку в каждой точке линии тока вектор скорости касателен к ней, то бесконечно малый элемент кривой ds и вектор скорости в данной точке можно рассматривать как параллельные прямые.

Рис.3.2.К основным понятиям кинематики жидкости:

а – линия тока; b – элементарная струйка; с − поток

Условие параллельности вектора ds с проекциями dx,dy,dz и вектора скорости с проекциями u_x , u_y , u_z можно записать как:

. (3.1)

Это выражение − уравнение линии тока.

Проведем в какой – либо точке линии тока элементарную площадку dω, перпендикулярную к линии тока (рис. 3.2, b). Она называется живым

сечением. Через каждую точку контура живого сечения проведем линии тока. Образованная этими линиями тока криволинейная цилиндрическая поверхность называется трубкой тока . Жидкость, заполняющая трубку тока, называется элементарной струйкой. При установившемся движении элементарная струйка обладает следующими свойствами:

• во всех точках данного живого сечения скорость можно считать одинаковой;

• соседние элементарные струйки не пересекаются и не перемешиваются;

• с течением времени форма элементарной струйки не изменяется.

Потоком жидкости называется вся совокупность элементарных струек, протекающих по данному каналу. Живым сечением потока называется часть его поперечного сечения, занятая жидкостью. В отличие от элементарной струйки, скорость по сечению потока переменна (рис. 3.2, с).

Потоки бывают напорными и безнапорными. Напорные потоки возникают при движении жидкости в условиях избыточного давления; живое сечение трубопровода полностью заполнено жидкостью; с окружающей средой жидкость сообщения не имеет. Безнапорные потоки возникают при движении жидкости за счет собственного веса − это движение в открытых каналах, имеющих уклон. Жидкость при этом имеет свободную поверхность, граничащую с окружающей средой.

Плавно изменяющееся движение потока − такое, при котором кривизна линий тока мала, угол расхождения между ними также мал. В этом случае сечение потока можно считать плоским.

Одномерными называются такие потоки, параметры которых (скорость и давление) зависят только от одной координаты (например, от продольной координаты x). Двумерным или плоским потоком называется такой, у которого параметры зависят от двух координат − продольной и одной из поперечных (например, x и z). У трехмерного потока параметры движения − функции трех координат. Если у трехмерного потока параметры в двух поперечных координатах изменяются одинаково, поток называется осесимметричным.

Объемным расходом или просто расходом Q называется объем жидкости, протекающей через живое сечение потока в единицу времени: , м³/с. Если речь идет о расходе элементарной струйки за бесконечно малый отрезок времени dt, то можно записать: .

Связь между скоростью и расходом. Рассмотрим вначале элементарную

струйку (рис. 3.3, а). В живом сечении dω₁ скорость равна u.

Рис.3.3. Связь между скоростью и расходом:

a , b – для элементарной струйки; c – для потока

Пусть за время dt жидкость, находящаяся в живом сечении dω₁ , пройдет путь ds и окажется в сечении dω₂ . Ввиду малости ds можно считать, что площадь не изменилась, то - есть dω₁ = dω₂ = dω . Объем жидкости, прошедший за dt через dω₁ , равен объему цилиндра: dW = ds∙dω. Разделим обе части этого выражения на dt:

.

Так как , а , то получим связь между скоростью и расходом

для элементарной струйки:

. (3.2)

Расход через сечение потока ω (рис. 3.3, с) можно найти, просуммировав

(то - есть проинтегрировав) расходы всех элементарных струек потока по всей

площади живого сечения:

. (3.3)

Для интегрирования необходимо знать закон изменения скорости по сечению потока (математическое описание подинтегральной функции u).

Для решения многих практических задач знание всей эпюры скоростей необязательно − достаточно знать среднюю скорость V потока в сечении .

Средней скоростью потока в данном сечении называется такая фиктивная скорость V, постоянная по всему сечению, при которой расход через данное сечение равен истинному, определяемому интегралом (3.3).

Заменим в выражении (3.3) u на V. Поскольку V = const, V можно вынести за знак интеграла и получить

Q = V∙ω . (3.4)

Это выражение определяет связь между расходом и средней скоростью для потока.

Уравнение постоянства расхода при установившемся движении

Рассмотрим вначале элементарную струйку несжимаемой жидкости

(ρ = const). Пусть два ее живых сечения dω₁ и dω₂ расположены на таком

расстоянии друг от друга, когда пренебречь различием в площадях dω₁ и dω₂

нельзя (рис. 3.3, b). За время dt через сечение dω₁ втекает в объем А дополнительный объем dW₁ = dQ₁ dt = u₁ d ω₁dt. За это же время через сечение

dω₂ вытекает объем dW₂ = dQ₂ dt = u₂ dω₂ dt. Очевидно, что dW₁ = dW₂ .

Если бы за отрезок времени в ограниченный объем струйки втекало жидкости больше, чем вытекало, струйка стала бы толще, если наоборот − тоньше.

Оба этих варианта противоречат свойству элементарной струйки сохранять свою форму при установившемся движении. Отсюда следует: dQ₁ = dQ₂ или

. (3.5)

Проведя аналогичные рассуждения для потока , имеющего в живых сечениях ω₁ и ω₂ средние скорости соответственно V₁ и V₂ , получим выражение для уравнения постоянства расхода для потока:

. (3.6)