4.10. Режимы течения

Движение жидкости может происходить, как впервые отметил Г.Хаген (1869 г.), в двух качественно различных режимах – ламинарном и турбулентном. Детальные экспериментальные исследования режимов выполнил О.Рейнольдс (1883 г.). Вводя струйку краски в поток, протекающий по трубе, он визуально определял форму линий тока; при этом измерялись расход и путевые потери на мерном участке трубы (рис. 4.16).

При малых скоростях линии тока параллельны оси трубы; движение происходит параллельными слоями (рис. 4.16, а). Такой режим движения называется ламинарным. При увеличении скорости линии тока вначале начинают искривляться, а затем происходит переход к беспорядочному, хаотическому движению с пересечением линий тока и перемешиванием

(рис. 4.16, b). Такой режим называется турбулентным. Смена режимов приводит к увеличению темпа роста путевых потерь при увеличении расхода.

Исследования показали, что наличие того или иного режима связано с численным значением критерия (здесь за характерную длину L принят диаметр трубы d): при (нижнее критическое число Re) режим ламинарный, при Re > 2300 начинается переход к турбулентному режиму; после достижения некоторого значения Re (верхнее критическое число Re) режим полностью турбулентный. Более поздние исследования показали, что как нижнее, так и верхнее критические значения Re зависят от многих причин и могут колебаться (нижнее – от 1000 до 2300, верхнее – от 3500 до

40 000). Для переходного режима надежных расчетных формул для определения гидравлических потерь не существует; поэтому на практике принято считать при Re ≤ 2300 режим ламинарным, при Re > 2300 – турбулентным.

4.11. Ламинарный режим течения

Рассмотрим установившееся равномерное движение жидкости в трубе круглого сечения вдоль оси х (рис. 4.17). За поперечную координату примем радиус r; это позволит рассматривать движение как двумерное.

В жидкости выделим цилиндрический объем радиусом r и длиной L. Так как

движение равномерное, объем находится в равновесии под действием сил давления на торцах (сечения 1−1 и 2−2), а также силы трения, вызванной действием касательных напряжений τ на боковой поверхности цилиндра.

Условие равновесия запишется в виде:

. (4.55)

Рис. 4.17. Движение жидкости в трубе при ламинарном режиме

Обозначив , из (4.55) получим:

. (4.56)

Эта формула определяет линейный закон распределения касательных напряжений по радиусу трубы, показанный на рисунке слева.

Найдем закон изменения скорости от радиуса трубы. Запишем формулу гипотезы Ньютона:

. (4.57)

Знак (−) поставлен потому, что с увеличением радиуса скорость падает (du<0).

Приравняем (4.56) и (4.57).

; ; .

Константу С найдем из граничного условия − при r = r₀ u = 0; . Отсюда . (4.58)

Получили параболоид вращения (рис. 4.17, справа).

Максимальная скорость (на оси трубы) равна:

. (4.59)

Найдем расход через кольцевое сечение радиусом r и толщиной dr:

.

Интегрируя, найдем общий расход через сечение ω:

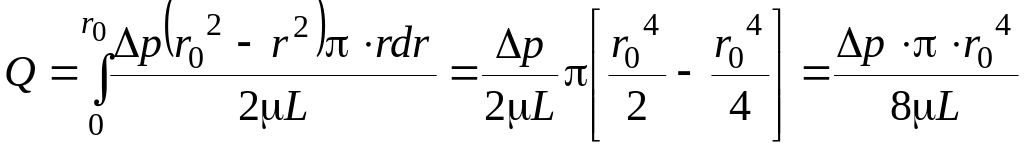. (4.60)

Найдем среднюю скорость в сечении V :

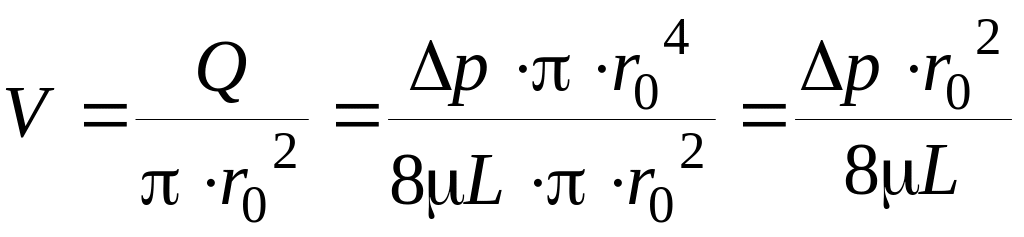. (4.61)

Сопоставляя (4.59) и (4.61), получим, что .

Найдем теперь коэффициент Кориолиса α в соответствии с (4.15):

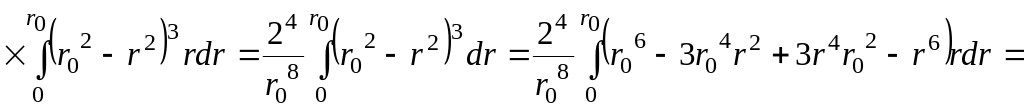
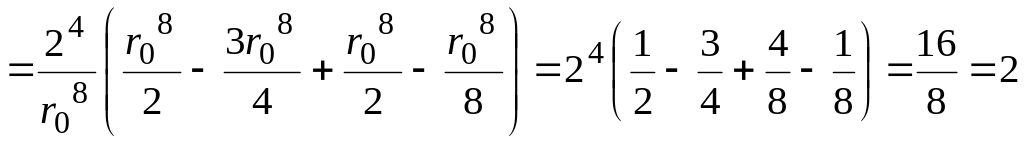. (4.62)

Выведем теперь формулу для λ в формуле Дарси.

Из формулы для V (4.61) получим:

. (4.63)

Чтобы разность давлений перевести в гидравлические потери в единицах напора (м), нужно Δр разделить на ρg :

. (4.64)

В полученной формуле числитель и знаменатель умножим на 2V и приравняем

это выражение путевым потерям, вычисляемым по формуле Дарси:

.

Учтя, что , получим:

.

Отсюда следует:

. (4.65)

Полученная формула называется формулой Хагена−Пуазейля.

Как следует из формулы (4.65), λ и путевые потери не зависят

от шероховатости трубы. Это объясняется тем, что при ламинарном режиме велико влияние сил вязкости. Тонкий неподвижный слой жидкости прилипает к стенке и покрывает ее неровности. Поэтому вышележащие слои, двигаясь, скользят по этому неподвижному слою, как по жидкой смазке.

Проверим, является ли ламинарное течение потенциальным, по условиям (3.23):

; ; .

В рассматриваемом случае , , .

Кроме того, выразим радиус через поперечные координаты:

; .

.

Следовательно, ламинарное течение является вихревым.

Ламинарное течение в трубе устанавливается постепенно (рис. 4.18).

Рис. 4.18. Начальный участок ламинарного течения в трубе

Длина трубы, на которой происходит формирование расчетной эпюры скоростей, называется начальным участком. Эта длина может быть определена по формуле Буссинеска:

. (4.66)