2.4 Сурет Шеңбер тектес поляризация: сол және оң жақ айналым

3. Егер φ=±90° және Е_ох≠Е_оу, Е векторы жазықтықта z=const бойынша айналады, бирақ оның ұзындығы өзгереді. Нәтижесінде Е векторының ұшы эллипсті сипаттайды , ал поляризация эллипс тектес поляризация деп аталады.(2.5 сурет). Фазаның жылжуы кезінде толқын элиппс тектес поляризация болып қала береді, бірақ эллипс осі х осіне γ бұрышына бұрылған (2.6 сурет), келесі формулада көрсетілген

(2.57)

Шеңбер тектес толқын поляризациясы радиотехника және байланыста кең қолданылады. Айналмалы поляризация толқының қозуы үшін мұндай толқынның екі сызықты-поляризанған векторлары Е кеңістікте ортогональді болатын, амплитудалары бойынша тең және фаза бойынша 90 градусқа жылжыған толқындардың қосылуынан туғанын ескерген жөн.

2.5 сурет Эллипс тектес поляризация 2.6 сурет х осі мен γ бұрышы бойынша эллипстің эллипс тектес поляризациясы

Сызықтық поляризацияланған толқынды кері бағытта айналған және Е векторының бирдей амплитудасы ретінде екі толқынның шеңбер тектес поляризациясын суперпозиция ретінде ұсынуға болады. Әр түрлі ось бойынша толқынның таралу шығысында векторлық диаграммалары (2.7 сурет) көркемдейді.

Рис.2.7 Векторлық диаграммалар

3. Екі ортаның шекарасында толқындық көріністердің тарауы

3.1. Еркін бағдарлы жазық толқындар

Алдыңғы парагафтарда декарталық жүйенің осьтерінде таралған жазық толқындарды қарастырған болатынбыз.

Орта шығындарсыз деп болжаймыз. Толқынның электрлік және магниттік құраушыларын қарастырайық.

Сурет. 3.1 Цилиндрлік жүйедегі жазық толқын

мұнда:

,

,

мұнда: ,

(3.1)

Толқынның бағытын айқындайтын бұрыш косинустары бағыттаушы деп аталады.

Фазалық жазықтықтың теңдеуі(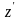 =const):

,

мұнда (3.2)

Онда скалярлық туындысы:

(3.3)

(3.4)

Орта шығынсыз деп болжаған болатынбыз. Ортада шығын болған жағдайда теңдеу өзгермейді, тек k-ның орнына =-j қойылады. Қарастырмай тұрып толқындық көріністерге анықтама берейік.

Жазықтық, шекараға нормаль арқылы қатарлас өтетін, құлау жазықтығы деп аталады. Вектор толқынның таралу бағытына перпендикуляр, ал толқынның құлау жазықтығына қатысты ол еркін түрде бағытталады.

Пікірлердің жалпы түрін жоғалтпай, вектор _{бағытының екі жағдайын қарастырсақ жеткілікті:}

1) _{векторы құлау жазықтығына перпендикуляр} (бір қалыпты поляризация);

2) _{векторы құлау жазықтығына параллель} (қатарлас поляризация).

Вектор _{-нің еркін бағыты кезінде, ол осы екі жағдайдың суперпозициясы түрінде түсіндіріледі.}