Гармоникалық жазықтықтың электродинамикалық потенциалдары
1.1. Гельмгольца теңдеуі
Электродинамиканың барлық есептері 2 түрге бөлінеді:
тура есептер, электромагнитті жазықтықта берілген есептер бойынша сәкесінше қажетті бөлшекті табуға болады;
кері есептер, берілген электромагнитті есептер бойынша, сәйкесінше керекті анықтамаларды алуға болады.
Бұл бөлімде тура және кері электродинамиканың есептерді шығару әдістерін қарастырмыз.
Есептердің көптігі соншалық жолақтағы векторды есептеп шығару өте қиын. Комплексты амплитуда әдісін пайдаланып гармоникалық жолақ үшін есепті шығаруға болады. Электродинамикадағы кез келген есепті шығару үшін Максвелл теңдеуін қолданамыз. Максвелл теңдеуін дифференциалды теңдеу формасына түрлендіруді теңдеу формасына түрлендіруді іске асырады. Гармоникалық электромагнитті процессті қарастырамыз. Максвелл теңдеуін комплексті амплитуда үшін жазамыз.
.
(1.1)
.
(1.2)
Оң жақ бөліктен сол жақ бөлікке роторды аламыз. (1.1).
Сонда
.
(1.3)
Белгілі теңдеуді қолданамыз
Максвеллның
төртінші теңдеуінен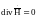
, яғни
.
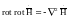(1.4)
Орнына
қоямыз (1.4)
және
(1.2) әрекеттесуі
(1.3) одан
шығатыны
немесе
,
(1.5)
сонда
к=
.
Сонымен жоғарыда келтірілген түрлендіруде біз бірдей емес дифференциалды теңдеуді алдық, математикалық физикадағы атауы Гельмгольцтың әр түрлі теңдеуі.Бұл теңдеу толқынды процестерді көрсетеді.
1.2. Гельгольцтың түрлі теңдеуін шешу.
Гельмголцтың
әртүрлі теңдеуін шешу үшін
векторлы функциясын кіргізеді оны
вектордың электрлі потенциалы деп
атайды.
Келесідей векторлы әдістер бар
и
(1.6)
Гельмгольцтың әртүрлі теңдеуін аламыз
.
(1.7)
(1.6)
теңдеуін
(1.7) теңдеуіне
қоямыз да, мына теңдеуді аламыз:
.
(1.8)
Суретін қарастырамыз. Жолақтың мінездемелік Р нүктесіндегі көлем сыртындағы V-ны анықтау қажет,сонымен көлем ішіндегі кез келген нүктеден Р нүктенің көлемінен үлкендеу қашықтықтан алу керек.
Рис 1.1 Жолақтың мінездемелік қасиетін анықтау
Көлемнің
ішінен V нүктесін Q және оның айналасында
қарапайым көлем тұрғызамыз V.
R — нүкте арасындағы қашықтық Q және
Р.Біз
жолақтың
қарқының іздейміз,
Р нүктесінен басқа да токтар әсер
етуде.Бұл қарқын
.
—
пропорционал кейбір орташа мән токтың
көлем нығыздығына байланысты.
көлемнің мөлшері
R қашықтығынан әлдеқайда алысырақ,
сондықтан
басқа да токтармен өтіп жатқан, оны
нүктелік негіз ретінде қарауға болады.
Симмерия күшінде жолақтың қарқының
бірдей изотропты жазықтықта нүктелік
негізін аттамалы фазасы теңбе тең, яғни
сфера түріне ие болады.
Қарапайым әдіспен қарағанда, жолақтың амплитудасы, нүктелік негіз r ғана тәуелді.
,
(1.9)
,
т.е.еш
жоғалусыз орта.
,
,
(1.10)
r — радиальды координат. Соңғы әрекеттесу сфералық толқынды суреттейді. Осы әдіспен, жазықтық осы токтармен әрекеттескендегі көлемі V .
.
(1.11)
Максвелл теңдеуі және одан шығатын Гельмгольца теңдеуі сызықты дифференциалды теңдеуі болып табылады, сондықтан оларға суперпозиция принципі дұрысырақ болып келеді. Бұл әдісте суперпозиция әдісі: жолақ, әр түрлі көлеммен әрекеттесуі, көлемнің ішінде V болуы, суперпозиция жазықтығын елестетуге болады, басқа да бір токтардың әрекетінен, ішіндегі қарапайым көлемнің өтуімен.
Теңбе тең пайда болу үшін, пропорционалды коэффициентті анықтау керек, V қарапайым көлемнің белгілі бір санның шексіз көбеюі соңғы нәтижеде анықталуы мүмкін. Математикалық физикада Гельмгольца теңдеуінің ортақ есебін шешкенде, бұл өту
.
(1.12)