
- •Астраханский Государственный технический Университет
- •Программа и контрольные задания по математике
- •Контрольные задания рассмотрены и одобрены на заседании кафедры протокол заседания № 6 от 12. 02 .2013г. Методические указания
- •Программа курса высшей математики
- •Литература
- •I. Линейная алгебра.
- •II. Векторная алгебра. Аналитическая геометрия.
- •III. Введение в математический анализ.
- •IV. Производная и дифференциал функции.
- •V. Приложения дифференциального исчисления.
- •VI. Дифференциальное исчисление функции нескольких переменных.
- •VII. Неопределенный и определенный интегралы.
- •VIII. Дифференциальные уравнения.
- •IX. Кратные и криволинейные интегралы.
- •X. Числовые и степенные ряды.
- •XI. Ряды Фурье. Математическая физика. Функция
- •XII. Теория вероятностей и математическая статистика.
VIII. Дифференциальные уравнения.
8.1. – 8.10. Найти общие решения дифференциальных уравнений первого порядка.
8.1.
а)
|
б)
|
8.2.
а) |
б)
|
8.3.
а)
|
б)
|
8.4.
а)
|
б)
|
8.5.
а)
|
б)
|
8.6.
а)
|
б)
|
8.7.
а)
|
б)
|
8.8.
а)
|
б)
|
8.9.
а)
|
б)
|
8.10.
а)
|
б)
|
8.11. – 8.20. Найти частное решение дифференциального уравнения второго порядка, удовлетворяющее начальным условиям.
8.11.
|
8.12.
|
8.13.
|
8.14.
|
8.15.
|
8.16.
|
8.17.
|
8.18.
|
8.19.
|
8.20.
|
IX. Кратные и криволинейные интегралы.
9.1. – 9.10. Дан двукратный интеграл. Изобразить на чертеже область интегрирования. С помощью этого интеграла найти ее площадь.
9.1.
|
9.2.
|
9.3.
|
9.4.
|
9.5.
|
9.6.
|
9.7.
|
9.8.
|
9.9.
|
9.10.
|
|
|
9.11.
– 9.20.
Вычислить двойной интеграл
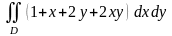 ,
где область интегрирования
,
где область интегрирования
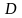 ограничена линиями
ограничена линиями
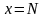 ,
,
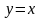
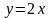 ,
где
,
где
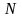 - номер варианта. Сделать чертеж.
- номер варианта. Сделать чертеж.
9.21.
– 9.30.
Вычислить тройной интеграл
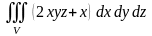 ,
где область интегрирования
,
где область интегрирования
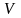 задана плоскостями
задана плоскостями
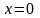 ,
,
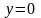 ,
,
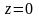 ,
,
,
,
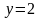 ,
,
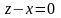 где
- номер варианта. Сделать чертеж.
где
- номер варианта. Сделать чертеж.
9.31.
Вычислить криволинейный интеграл
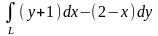 вдоль дуги
вдоль дуги
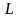 окружности
окружности
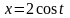 ,
,
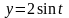 от точки
от точки
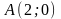 до точки
до точки
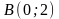 ,
обходя ее против часовой стрелки.
,
обходя ее против часовой стрелки.
9.32.
Вычислить криволинейный интеграл
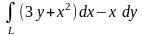 вдоль дуги
параболы
вдоль дуги
параболы
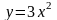 от точки
от точки
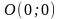 до точки
.
до точки
.
9.33.Вычислить
криволинейный интеграл
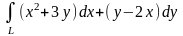 вдоль дуги
параболы
вдоль дуги
параболы
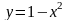 от точки
от точки
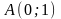 до точки
до точки
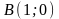 .
.
9.34.
вычислить криволинейный интеграл
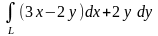 вдоль
– эллипса
вдоль
– эллипса
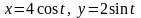 ,
обходя его против часовой стрелки.
,
обходя его против часовой стрелки.
9.35.
Вычислить криволинейный интеграл
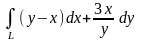 вдоль дуги
кривой
от точки
до точки
вдоль дуги
кривой
от точки
до точки
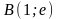 .
.
9.36.
Вычислить криволинейный интеграл
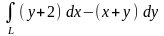 вдоль прямой
вдоль прямой
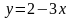 от точки
от точки
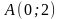 до точки
до точки
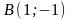 .
.
9.37. Вычислить криволинейный интеграл
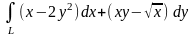 вдоль дуги
параболы
вдоль дуги
параболы
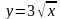 от точки
до точки
.
от точки
до точки
.
9.38.
Вычислить криволинейный интеграл
 вдоль дуги
кривой
вдоль дуги
кривой
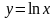 от точки
до точки
от точки
до точки
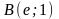 .
.
9.39. Вычислить криволинейный интеграл
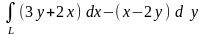 вдоль прямой
вдоль прямой
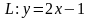 от точки
от точки
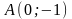 до точки
до точки
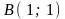 .
.
9.40. Вычислить криволинейный интеграл
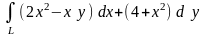 вдоль дуги
гиперболы
вдоль дуги
гиперболы
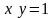 от точки
от точки
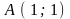 до точки
до точки
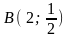 .
.

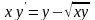 ;
;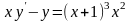 .
.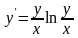 ;
;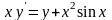 .
.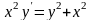 ;
;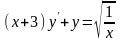 .
.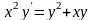 ;
;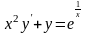 .
.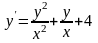 ;
;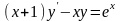 .
.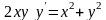 ;
;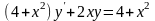 .
.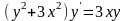 ;
;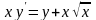 .
.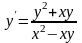 ;
;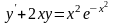 .
.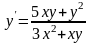 ;
;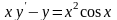 .
.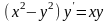 ;
;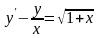 .
.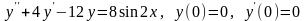 .
.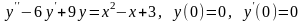 .
.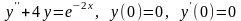 .
.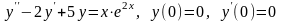 .
.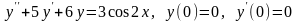 .
.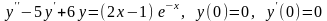 .
.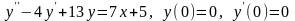 .
.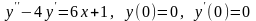 .
.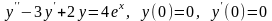 .
.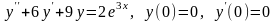 .
.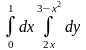 ;
;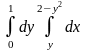 ;
;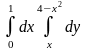 ;
;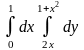 ;
;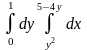 ;
;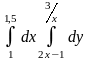
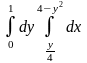 ;
;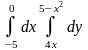 ;
;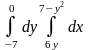
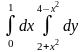 .
.