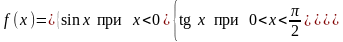- •Астраханский Государственный технический Университет
- •Программа и контрольные задания по математике
- •Контрольные задания рассмотрены и одобрены на заседании кафедры протокол заседания № 6 от 12. 02 .2013г. Методические указания
- •Программа курса высшей математики
- •Литература
- •I. Линейная алгебра.
- •II. Векторная алгебра. Аналитическая геометрия.
- •III. Введение в математический анализ.
- •IV. Производная и дифференциал функции.
- •V. Приложения дифференциального исчисления.
- •VI. Дифференциальное исчисление функции нескольких переменных.
- •VII. Неопределенный и определенный интегралы.
- •VIII. Дифференциальные уравнения.
- •IX. Кратные и криволинейные интегралы.
- •X. Числовые и степенные ряды.
- •XI. Ряды Фурье. Математическая физика. Функция
- •XII. Теория вероятностей и математическая статистика.
II. Векторная алгебра. Аналитическая геометрия.
2.1.
– 2.10. Даны
координаты четырех точек
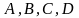 .
Требуется средствами векторной алгебры
найти: 1) угол между векторами
.
Требуется средствами векторной алгебры
найти: 1) угол между векторами
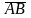 и
и
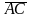 ;
2) площадь треугольника
;
2) площадь треугольника
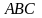 ;
3) объем пирамиды
;
3) объем пирамиды
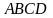 ;
4) сделать схематический чертеж.
;
4) сделать схематический чертеж.
2.1.
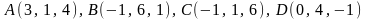 .
.
2.2.
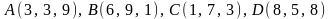 .
.
2.3.
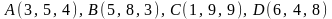 .
.
2.4.
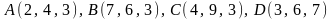 .
.
2.5.
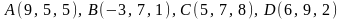 .
.
2.6.
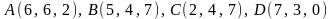 .
.
2.7.
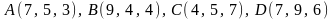 .
.
2.8.
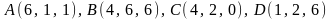 .
.
2.9.
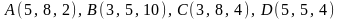 .
.
2.10.
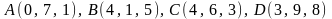 .
.
2.11.
– 2.20. Даны
уравнения плоскости
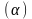 и координаты точки
и координаты точки 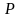 .
Требуется найти: 1) канонические уравнения
прямой
.
Требуется найти: 1) канонические уравнения
прямой
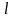 ,
проходящей через точку
перпендикулярно плоскости
;
2) точку пересечения прямой
с плоскостью
;
3) уравнение плоскости, проходящей через
прямую
и начало координат. Сделать схематический
чертеж.
,
проходящей через точку
перпендикулярно плоскости
;
2) точку пересечения прямой
с плоскостью
;
3) уравнение плоскости, проходящей через
прямую
и начало координат. Сделать схематический
чертеж.
2.11.
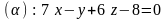 ,
,
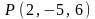 .
.
2.12.
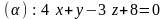 ,
,
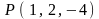 .
.
2.13.
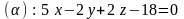 ,
,
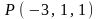 .
.
2.14.
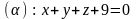 ,
,
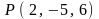 .
.
2.15.
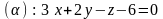 ,
,
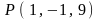 .
.
2.16.
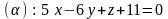 ,
,
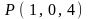 .
.
2.17.
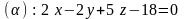 ,
,
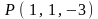 .
.
2.18.
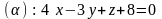 ,
,
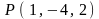 .
.
2.19.
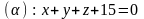 ,
,
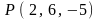 .
.
2.20.
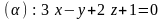 ,
,
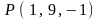 .
.
2.21.
Составить
уравнение прямой, проходящей через
начало координат и точку пересечения
прямых
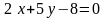 и
и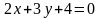 .
Сделать чертеж.
.
Сделать чертеж.
2.22.
Найти уравнения перпендикуляров к
прямой
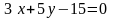 ,
проведенных через точки пересечения
данной прямой с осями координат. Сделать
чертеж.
,
проведенных через точки пересечения
данной прямой с осями координат. Сделать
чертеж.
2.23.
Даны уравнения
сторон четырехугольника:
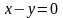 ,
,
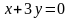 ,
,
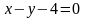 ,
,
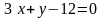 .
Найти уравнения его диагоналей. Сделать
чертеж.
.
Найти уравнения его диагоналей. Сделать
чертеж.
2.24.
Найти
уравнения высот треугольника
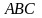 ,
проходящих через вершины
и
,
если
,
проходящих через вершины
и
,
если
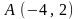 ,
,
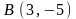 ,
,
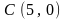 .
Сделать чертеж.
.
Сделать чертеж.
2.25.
Найти координаты точки пересечения
перпендикуляров, проведенных через
середины сторон, треугольника, вершинами
которого служат точки
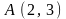 ,
,
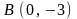 ,
,
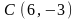 .
Сделать чертеж.
.
Сделать чертеж.
2.26.
Найти уравнение высоты, проведенной
из вершины
треугольника
,
если уравнения его сторон:
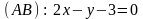 ,
,
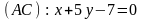 ,
,
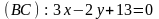 .
Сделать чертеж.
.
Сделать чертеж.
2.27.
Через точку пересечения прямых
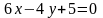 ,
,
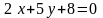 ,
провести прямую, параллельную оси
абсцисс. Сделать чертеж.
,
провести прямую, параллельную оси
абсцисс. Сделать чертеж.
2.28.
Найти точку
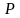 пересечения диагоналей четырехугольника
,
если
пересечения диагоналей четырехугольника
,
если
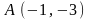 ,
,
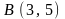 ,
,
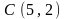 ,
,
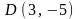 .
Сделать чертеж.
.
Сделать чертеж.
2.29.
Доказать, что четырехугольник
– трапеция, если
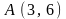 ,
,
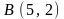 ,
,
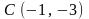 ,
,
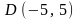 .
Сделать чертеж.
.
Сделать чертеж.
2.30.
Найти
уравнение прямой, проходящей через
точку
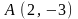 и точку пересечения прямых
и точку пересечения прямых
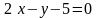 и
и
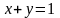 .
Сделать чертеж.
.
Сделать чертеж.
III. Введение в математический анализ.
3. 1. – 3.10. Найти пределы функций, не пользуясь правилом Лопиталя.
3.1.
а)
|
б)
|
в)
|
г)
|
3.2.
а)
|
б)
|
в)
|
г)
|
3.3.
а)
|
б)
|
в)
|
г)
|
3.4.
а)
|
б)
|
в)
|
г)
|
3.5.
а)
|
б)
|
в)
|
г)
|
3.6.
а)
|
б)
|
в)
|
г)
|
3.7.
а)
|
б)
|
в)
|
г)
|
3.8.
а)
|
б)
|
в)
|
г)
|
3.9.
а)
|
б)
|
в)
|
г)
|
3.10.
а)
|
б)
|
в)
|
г)
|
3.11.
– 3.20. Задана
функция
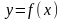 .
Требуется: 1) исследовать на непрерывность;
2) классифицировать точки разрыва
функции, если они существуют; 3) исследовать
поведение функции на бесконечности;
4) сделать схематический чертеж по
результатам исследования.
.
Требуется: 1) исследовать на непрерывность;
2) классифицировать точки разрыва
функции, если они существуют; 3) исследовать
поведение функции на бесконечности;
4) сделать схематический чертеж по
результатам исследования.
3.11.
а)
|
б)
|
3.12. а)
|
б)
|
3.13.
а)
|
б)
|
3.14.
а)
|
б)
|
3.15.
а)
|
б)
|
3.16.
а)
|
б)
|
3.17.
а)
|
б)
|
3.18.
а)
|
б)
|
3.19.
а)
|
б)
|
3.20.
а)
|
б)
|

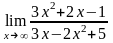 ;
;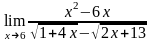 ;
;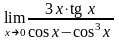 ;
;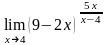 .
.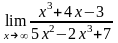 ;
;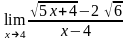 ;
;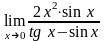 ;
;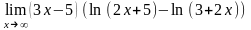 .
.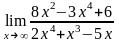 ;
;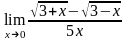 ;
;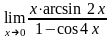 ;
;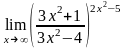 .
.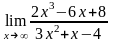 ;
;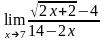 ;
;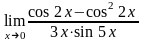 ;
;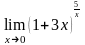 .
.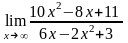 ;
;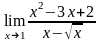 ;
;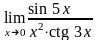 ;
;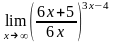 .
.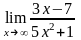 ;
;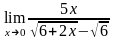 ;
;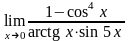 ;
;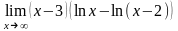 .
.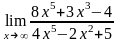 ;
;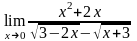 ;
;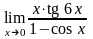 ;
;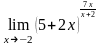 .
.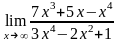 ;
;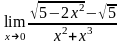 ;
;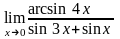 ;
;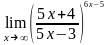 .
.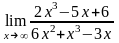 ;
;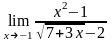 ;
;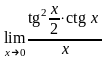 ;
;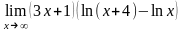 .
.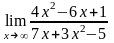 ;
;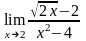 ;
;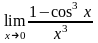 ;
;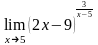 .
.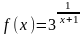 ;
;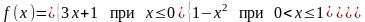 .
.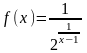 ;
;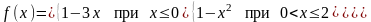 .
.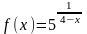 ;
;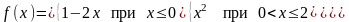 .
.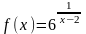 ;
;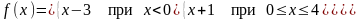 .
.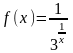 ;
;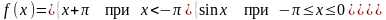 .
.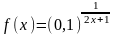 ;
;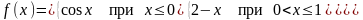 .
.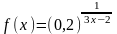 ;
;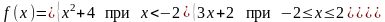 .
.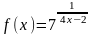 ;
;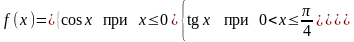 .
.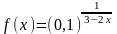 ;
;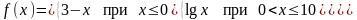 .
.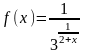 ;
;