
Лабораторные работы / Lektsia_Dinamicheskie_kh-ki_rakety_kak_tverdogo_tela
.pdf
Для обеспечения управления и устойчивости движения в системе стабилизации ракеты используются сигналы от чувствительных элементов, пропорциональные ускорениями в направлении продольной и поперечной осей ракеты. Эти сигналы
определяются непосредственно из уравнений движения в связанной системе координат.
Проекции скорости на оси Ox1 и Oy1 связанной системы координат будут (см. рис.
1.5) x1 cos , y1 sin . Для этой системы координат в уравнениях (1.12) и (1.13)
нужно принять, что z1 |
0, y x 1 |
2 |
0, 3 z . Тогда получим |
||||||||||||||
m( |
x1 |
|
y1 |
) (P X |
p |
) X cos Y sin G sin X ' |
, |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
в |
|
||||
m( |
y1 |
|
x1 |
) Y cos X sin G cos Y |
p |
Y ' , |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
в |
|
|||
I M |
a |
M |
д |
Y |
(x |
p |
x |
м |
) M ' , |
|
|
|
|||||
z |
|
|
|
|
p |
|
|
|
в |
|
|
|
|||||
x cos ,
tg y1 .x1
Здесь Xв' ,Yв' , Mв' – некоторые возмущающие силы и момент, которые будем считать
заданными.
Чтобы найти решение уравнений (1.14) или (1.15), нужно знать закон изменения по времени управляющих сил Yp (t) . Закон задается системой управления и зависит от типа и структуры этой системы. Уравнение системы управления можно представить в виде
(t) ( , ,..., y )
Уравнения (1.14) и (1.15) получены в предложении, что стартовая система координат инерциальна. Вращение стартовой системы координат вместе с Землей приводит, вообще говоря, к необходимости учитывать переносной aпер и кориолисово aк
ускорения ракеты (4).

3. О расчете траектории движения ракеты
Если считать закон изменения во времени угла поворота управляющих органов
= ( ) заданным, то из уравнений (1.14) для любого момента времени можно определить скорость и угол θ, а из равенств:
x0 t |
cos dt, |
y0 t |
sin dt |
0 |
|
0 |
|
вычислить координаты центра масс в системе Ax0 y0 z0 , т.е. траекторию ракеты. Однако
уравнения (1.14) являются нелинейными уравнениями с переменными коэффициентами и их решение сопряжено с большими трудностями.
При практических расчетах траектории полета и параметров невозмущенного движения уравнения (1.14) подвергают значительному упрощению. Так как программное движение ракеты совершается с незначительными угловыми скоростями и ускорениями,
то можно |
положить, что угловая скорость и ускорение в программном |
движении пр |
пр 0 . В этом случае третье уравнение (1.14) будет представлять собой |
уравнение равновесия между аэродинамическим моментов и моментом от управляющих сил, называемое балансировочным уравнением.
qlScm пр Rp (xp xм ) пр ,
где – расстояние от вершины ракеты до точки приложения управляющей силы. Из этого уравнения можно определить программный угол поворота рулей пр, который необходим для поддержания требуемого программного угла атаки пр. При расчетах траектории и параметров невозмущенного движения систему управления считают идеальной, закон изменения углов поворота управляющих органов считается совпадающим с программным.

Рис. 1.6
Если форма траектории, т.е. зависимость угла пр наклона касательной от времени полета, известна заранее, то второе уравнение (1.14) может служить при определении потребного угла атаки для обеспечения заданной траектории:
|
|
|
пр g cos пр |
|
|
|
|
||||||
пр |
|
|
|
|
|
|
|
|
|
|
|
|
. |
P X p |
2 |
|
|
l |
cm |
|
|||||||
|
|
S cy |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
xp |
xм |
|
|
||||||
|
|
|
|
|
|
|
|||||||
Так как угол атаки баллистических ракет в полете обычно мал, то в первом приближении им можно пренебречь и рассчитывать траекторию при α=0. Поэтому наиболее простые уравнения для расчета скорости , ускорения ̇и траектории будут иметь вид:
|
1 |
|
|
|
2 |
|
|
|
|
|
P X p |
|
|
|
|
Scx |
g sin пр . |
|
|
|
|
|||||
|
m |
|
|
2 |
|
|
|
|
|
t |
|
|
|
|
|
t |
|
x0 cos пр dt, |
y0 |
sin пр dt. |
||||||
|
0 |
|
|
|
|
0 |
|
|
В этом случае ошибка, с которой определяется ускорение ̇, меньше на 10-20%, чем ошибка от неточного значения коэффициента .
Если расчет траектории производится на дальность более 50 км, то необходимо учитывать кривизну поверхности Земли. Связь между координатами x0, y0, хордой L дуги окружности Земли и местной высотой Н можно определить из следующих геометрических соотношений (рис. 1.6):
(R0 H ) cos R0 y0 ,
|
|
|
|
|
|
0, |
x0 H sin L cos |
|
|||||
|
|
|
|
2 |
|
|
|
|
|
L |
|
|
|
sin |
|
|
. |
|
|
|
|
|
|
||||
2 |
|
|
2R0 |
|
|
|
Кроме того, для более точного определения полной дальности полета необходимо учитывать ускорение Кориолиса.
4. Уравнение возмущенного движения
Как было упомянуто выше, действительное движение всегда будет отличаться от программного. Причины, вызывающие отклонение движения от программного, будем называть возмущающими факторами. Эти факторы могут быть как постоянными, так и случайными.

Искажение внешней геометрии корпуса, несоосность двигателя с корпусом,
отклонение от расчетных значений тяги двигателя я стартового веса, изменение эффективности органов управления ракеты н другие факторы действуют постоянно и являются для заданной ракеты систематически действующими возмущающими
факторами. Эти возмущения могут быть учтены в уравнениях (1.14) членами Xв ,Yв , Mв .
Так как возмущающие факторы Xв ,Yв , Mв для разных ракет могут быта различными,
то действительные траектории и параметры Движения на управляемом участке будут как
бы «заключены» в трубку, осью для которой является программная траектория.
Движение ракеты в трубке траекторий будем называть номинальным движением. По характеристикам возмущений можно установить размеры трубки траекторий, которые
являются исходными для расчета рассеивания.
Кратковременные возмущения, такие как порывы ветра, кратковременные изменения тяги двигателя, помехи и ложные сигналы в системе управления, обычно случайны и их невозможно учесть в уравнениях движения, хотя они и оказывают влияние из движения ракеты. Это объясняется тем, что величина и время действия этих случайных
возмущающих факторов неизвестны.
Под воздействием этих случайных возмущений изменяются параметры движения,
поэтому величину любого из них можно представить состоящей из номинального значения (без учета возмущения) и некоторого малого отклонения, называемого
возмущением: |
|
в н , в н , в н , в н , в н . |
(1.17) |
Уравнения (1.14) н (1.15) справедливы для произвольных функций в , в , в , в в
частности, они справедливы и для функций номинального движения н , н , н , н .
Обычно при линеаризации уравнений движения пренебрегают влиянием приращения высоты на аэродинамические силы и моменты, а также на силу тяги
двигателя, так как это влияние за небольшой промежуток времени незначительно.
Значения переменных из равенств (1.17) подставим в уравнения (1.14) и из полученного результата вычтем уравнения (1.14), соответствующие параметрам
номинального движения. Примем, что cos пр |
1, sin пр пр . |
Полагая |
возмущения |
, , , , малыми и оставляя только члены |
первого порядка, |
получим |
следующие |
уравнения в скоростной системе координат относительно возмущений: |
|
||

m Pэ н н Scx G cos н Ryp (н н ),
m н Pэ Gsin н н 2 2
|
|
н |
2 |
|
|
|
|
|
|
|
н |
|
|
2 |
(1.18) |
I |
|
|
|
Sc |
|
Sc |
|
|
|
|
Sc l |
|
|||
|
|
|
|
|
|
|
|||||||||
z |
2 |
|
m |
|
|
н |
m |
н |
2 |
|
|
m |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
l |
|
|
|
Ryp (xp |
xм ) |
Scml2 н 2 mcj |
п |
(x xм )dx . |
|
||||||||||
2 |
|
||||||||||||||
|
|
|
|
|
|
|
|
( j ) |
|
x0 j |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Здесь неизвестными являются возмущения параметров движения , ,, , . Функции
н ,н ,н ,н ,н характеризующие номинальное движение, считаются известными, их можно определить из решения уравнений (1.14) и уравнения (1.16). Так как номинальное движение мало отличается от программного, то в уравнениях (1.18) вместо номинальных значений можно принять программные значения о пр , пр , пр , пр , известные из расчета программного движения. Тогда уравнения (1.18) запишем в виде
c c c c 0, |
|
|||||
|
|
|
|
|
|
|
c c |
c |
c 0, |
(1.19) |
|||
|
|
|
|
|
|
|
c c c c c 0. |
|
|||||
|
|
|
|
|
|
|
Здесь введены следующие обозначения коэффициентов:
в первом уравнении
c m1 н Scx ,
c m1 (G cos н Pэ н Ryp н ),
(1.20)
c m1 (Pэ н Ryp н ), c m1 Ryp н ;
Во втором и третьем уравнениях
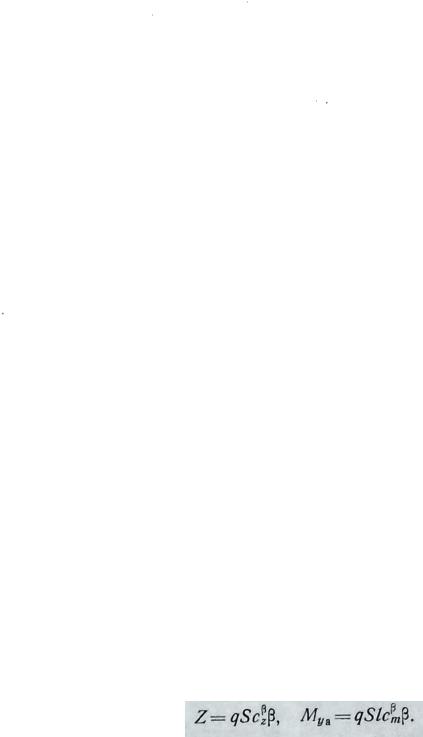
c
c
c
c
c
c
c
c
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
н |
Scy |
Ryp н н |
||||||||||||||
|
|
|
Pэ Gsin н |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
m н |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
||||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
н |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
Pэ |
|
|
Scy Ryp н н , |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m н |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
1 |
|
|
|
|
Sc |
|
, |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
н |
н |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
m н |
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
1 |
|
|
R |
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
m н |
yp |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
1 |
|
|
|
н |
Slcm 2 mc j |
lп |
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
(x xm )dx |
|
, |
||||||||||||||||||||||||
|
|
I |
|
|
|
|
2 |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(i ) |
|
|
x0 j |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
1 |
|
|
2н |
Sc |
c , |
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
I |
|
|
|
2 |
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
н Scm |
н |
|
|
|
Sl 2cm н , |
|
|
|
|||||||||||||||||
|
|
I |
|
2 |
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
1 |
R |
|
(x |
|
x ), I I |
|
. |
|
|
|
|
|
||||||||||||||||||
|
|
p |
z |
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
I |
|
|
|
|
yp |
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
,
(1.21)
В отличие от уравнений (1.14) уравнения (1.19) называются уравнениями возмущенного движения, или уравнениями в вариациях. Это линейные дифференциальные уравнения с переменными коэффициентами. Коэффициенты уравнений определяются через характеристики ракеты m, I, Pэ , Ryp , xp , xm параметры невозмущенного движения
н , н , н , н , н плотность воздуха и аэродинамические коэффициенты и могут быть
вычислены.
Теперь найдем уравнения возмущенного движения ракеты в скоростной системе координат в плоскости рысканья.
Невозмущенное движение ракеты происходит в плоскости тангажа, поэтому в плоскости рысканья все параметры номинального движения и внешние силы тождественно равны нулю. Возмущения в плоскости рысканья будем считать малыми и определять их через угол рысканья , угол скольжения , угол поворота траектории по отношению к плоскости невозмущенного движения и угол поворота управляющих органов .
Ввиду малости возмущений и наличия плоскостей симметрии ракеты возмущенное движение в плоскости рысканья не будет зависеть от возмущений в плоскости тангажа.
С появлением угла скольжения возникает поперечная аэродинамическая сила Z и
аэродинамический момент M ya , равные:

При этом вследствие осевой симметрии корпуса ракеты при н 0 производная
cz cy , cm cm .
При вращении корпуса ракеты с угловой скоростью возникает демпфирующий момент в плоскости рысканья. На основании уравнений (1.3) и (1.4).
Уравнения возмущенного движения в плоскости рысканья можно получить из уравнений (1.18), заменив в них вариации , , вариациями , , соответственно и
приняв G 0, н н н 0 . В этом случае второе и третье уравнения не будут связаны с первым уравнением. Итак, уравнения возмущенного движения в скоростной системе координат будут иметь вид
При принятых ранее допущениях малое возмущение в плоскости крена будет зависеть только от возмущений углов поворота управляющих органов. Момент управляющих сил рулей относительно продольной оси ракеты
M xp M xp x ,
где x – обобщенный угол поворота управляющего органа относительно продольной оси
Ox1; M xp —градиент управляющего момента.
Уравнение возмущенного движения относительно продольной оси будет

c |
c |
|
|
0, c |
|
1 |
M . |
(1.24) |
x |
|
|||||||
|
|
|
|
|
|
xp |
|
|
|
|
|
|
|
|
Ix |
|
|
Здесь через Ixc обозначен демпфирующий момент относительно продольной оси,
который может возникать, например, при наличии на корпусе ракеты оперения.
Найдем уравнения возмущенного движения ракеты в плоскости тангажа в связанной системе координат. Уравнения в этой системе координат необходимы для анализа ускорений, измеряемых чувствительными элементами системы стабилизации, по-
скольку ориентация чувствительных элементов связана с геометрическими осями корпуса ракеты.
Полагая в (1.15) x1в x1н x1, y1в y1н y1 принимая во внимание (1.17),
получим уравнения возмущенного движения в связанной системе координат Ox1 y1 :
Выразим через и через x1 и y1 . Так как x1 cos , y1 sin
С точностью до бесконечно малых величин второго порядка
Пренебрегая величиной н2 , находим

(1.26)
Заменив в (1.25) вариации в и а их выражениями из (1.26), получим уравнения возмущенного движения в связанной системе координат:
где введены следующие обозначения коэффициентов:
в первом уравнении
c' x x m1 н Scx ,
c' x y н m1 2 н S н (2cy сx ), c' x m1 G cos н ,
c' x н н ;
во втором равнении
В |
формулах (1.28) в (1.29) вследствие малости опущены члены, пропорциональные |
||
2 |
, |
, 3 |
. Для третьего уравнения вариация угла атаки определена по формуле |
н |
н н |
н |
|
y1 .н
Поэтому

c' |
|
1 |
2 |
Sl(c |
|
|
lc |
|
|||||||||
|
|
|
|
|
|
н |
|
m н |
), |
|
|||||||
|
|
|
|
|
|
|
н |
|
|
||||||||
x |
|
I н |
2 |
|
|
m |
|
|
н |
|
|||||||
|
|
|
|
|
|
|
|
(1.30) |
|||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
||
c' |
|
1 |
|
Slc |
|
|
I I |
|
|
|
|||||||
|
|
|
|
|
|
н |
, |
. |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|||||||||
y |
|
|
I н |
|
|
2 |
|
m |
|
|
|
z |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Уравнения в связанной системе координат для плоскости рысканья можно получить из 1.27 – 1.30, положив в них у1 z1, , , н н 0, G 0.
Для изучения короткопериодических возмущений на протяжении небольшого интервала времени будем в дальнейшем принимать траекторию невозмущенного движения центра масс ракеты прямолинейной. Составим уравнения возмущенного движе-
ния для плоскости тангажа в неподвижной системе координат. Такие уравнения более удобны при изучении возмущенного движения ракеты с учетом колебаний жидкости и
упругих колебаний корпуса.
Ось Ох неподвижной системы координат направим по касательной к траектории
невозмущенного движения, ось Оу — перпендикулярно ей (рис. 1.7).
Невозмущенное движение в плоскости тангажа в неподвижной системе координат
характеризуется следующими уравнениями: |
|
m xн Pэ cos н Gsin н X н Yр.н sin н , хн |
н , |
ун 0, Yн Pэ sin н G cos н Yр.н cos н 0 |
(1.31) |
н 0, M a.н Yр.н (xp xм ) 0. |
|
Обозначим малые возмущения проекций скорости центра масс на неподвижные оси координат через x и y малое возмущение угла тангажа через , а угла поворота управляющего органа через . В результате возмущений вектор скорости отклонится на угол y н , так что новое значение угла атаки
|
|
|
|
, у |
. (1.32) |
|
в |
|
н |
|
н |
|
|
|
|
Плоское движение в неподвижной системе координат Oxy определяется следующим уравнениями:
