15.2. Дисперсия случайной величины и ее свойства. Среднее квадратичное отклонение случайной величины.

Обозначение. Число 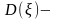дисперсия случайной величины .

Определение. .

Дисперсия случайной величины это мера рассеяния значений этой случайной величины вокруг ее математического ожидания.

Перечислим основные свойства дисперсии.

Свойство 1. Вычисление.

1)Если дискретная случайная величина,

то .

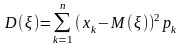2) Если непрерывная случайная величина,

то .

Свойство 2. Механический смысл дисперсии.

1) дискретная случайная величина.

На числовой прямой в точках поместим массы , .

центр масс системы этой системы материальных точек.

момент инерции этой системы материальных точек относительно оси, проходящей через точку перпендикулярно числовой прямой.

2) непрерывная случайная величина.

Заполним числовую прямую массой с линейной переменной плотностью . Получится тонкая бесконечная проволока.

центр масс этой проволоки.

момент инерции этой проволоки относительно оси, проходящей через точку перпендикулярно числовой прямой.

Свойство 3.Если для любого , то . Обычно коротко пишут: .

Свойство 4. , .

Свойство 5. , .

Свойство 6. 1) , если независимы;

2) , если независимы.

Свойство 7. Вычисление.

, где:

1) , если дискретная случайная величина;

2) , если непрерывная случайная величина.

Свойство 8. .

Определение. 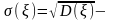среднее квадратичное отклонение случайной величины.

это тоже мера рассеяния значений этой случайной величины вокруг ее математического ожидания. Величина лучше дисперсии , так как она похожа на евклидово расстояние между точками.

§16. Избранные случайные величины. Нормальное распределение.

Определение. Пусть непрерывная случайная величина с плотностью вероятности

.

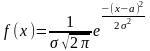Говорят, что эта случайная величина имеет нормальное распределение с параметрами и .

Перечислим основные свойства случайной величины с нормальным распределением.

Свойство 1. Нахождение плотности вероятности .

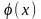, где . Следует почеркнуть, что функция четная функция, т.е. . Значения функции можно найти с помощью калькулятора или по таблице из приложения 1 задачника В.Е. Гмурмана.

Свойство 2. Нахождение функции распределения непрерывной случайной величины .

, где 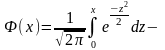функция Лапласа. Значения функции можно найти по таблице из приложения 2 задачника

В.Е. Гмурмана или с помощью программы MATHCAD−14:

.

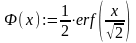Следует подчеркнуть, что функция нечетная функция, т.е. .

Свойство 3. Построение графиков функций и , и .

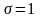Свойство 4. .