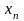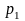§13. Дискретная случайная величина. Ряд распределения.

Определение. Пусть случайная величина. Она называется дискретной случайной величиной, если все ее значения образуют возрастающую последовательность вещественных чисел: .

Определение. Пусть дискретная случайная величина и есть последовательность всех ее значений. , . Таблица чисел

k	1	2	...
			...
			...

называется рядом распределения дискретной случайной величины . В этой таблице всегда и .

Теорема 13.1. Пусть дискретная случайная величина и дан ее ряд распределения

k	1	2	...
			...
			...

Тогда верны утверждения:

1)функция распределения равна

;

2) , .

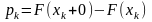§14. Непрерывная случайная величина. Плотность вероятности.

Определение. Пусть случайная величина. Она называется непрерывной случайной величиной, если существует функция такая, что всюду на множестве :

; .

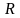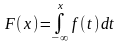Функция называется плотностью (распределения) вероятности непрерывной случайной величины .

Предположим, что функция распределения случайной величины всюду на множестве дифференцируема. Тогда верны следующие свойства непрерывной случайной величины:

1) всюду на множестве ;

2) ;

3) функция распределения 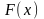всюду на множестве непрерывна;

4) ;

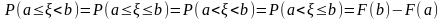5) .

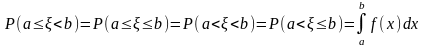Считается, что в свойствах 4 и 5

, .

Если же всюду дифференцируема на множестве , где конечное множество, то первое свойство выглядит так:

всюду на множестве . Остальные свойства не меняются.

В точках множества функция доопределяется любыми неотрицательными числами.

§15. Числовые характеристики случайных величин.

Пусть случайная величина.

1)Если дискретная случайная величина, то считается, что дан ее ряд распределения, где и .

k	1	2	...
			...
			...

2) Если непрерывная случайная величина, то считается, что дана ее плотность вероятности, где и .

15.1. Математическое ожидание случайной величины и его свойства.

Обозначение. Число 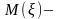математическое ожидание случайной величины .

Определение.

1) Если дискретная случайная величина, то .

2) Если непрерывная случайная величина, то .

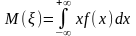Перечислим основные свойства математического ожидания.

Свойство 1. Механический смысл математического ожидания.

1) дискретная случайная величина.

На числовой прямой в точках поместим массы , . Тогда центр масс системы этой системы материальных точек.

2) непрерывная случайная величина.

Заполним числовую прямую массой с линейной переменной плотностью . Получится тонкая бесконечная проволока. Тогда центр масс этой проволоки.

Синонимы термина «математическое ожидание случайной величины»: среднее значение случайной величины; центр группирования значений случайной величины; истинное значение случайной величины (в старых учебниках).

Свойство 2.Если для любого , то . Обычно коротко пишут: .

Свойство 3. , .

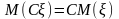Свойство 4. 1) ;

2) .

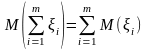Свойство 5. Пусть новая случайная величина, где 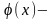числовая функция одной переменной, заданная на множестве значений старой случайной величины . Тогда верны утверждения:

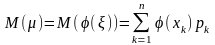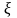1) , если и 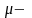дискретные случайные величины.

2) , если и непрерывные случайные величины.

Свойство 6.

Определение.

Случайные величины 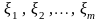называются независимыми, если

для любых вещественных чисел .

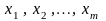На практике, как правило, математическая независимость случайных величин совпадает с их жизненной независимостью. Перейдем к формулировке свойства 6:

, если независимы.