§11. Случайные величины. Основные определения.

Пусть в результате некоторого испытания появилось множество , которое мы назвали пространством элементарных событий. Затем была выбрана некоторая алгебра событий (если можно, то 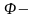максимальная алгебра событий). После этого для любого события из алгебры событий введена вероятность события так, что выполнены все четыре аксиомы А.Н. Колмогорова.

Определение. Вещественная функция , заданная на множестве называется случайной величиной.

Другими словами, случайная величина 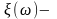это зависимость вещественных чисел от элементарных событий. Понятно, что у случайной величины множество (пространство элементарных событий) это область определения случайной величины, а множество вещественных чисел ее область изменения (область изменения содержит и множество всех значений случайной величины).

Таким образом, каждому элементарному событию ставится в соответствие единственное число .

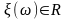Так как вещественные числа отождествляются с точками числовой прямой, то каждому элементарному событию ставится в соответствие единственная точка на этой прямой с координатой .

В частности, если , то случайная величина это обычная вещественная функция, которой было уделено так много внимания в курсе средней школы. Для случайных величин, у которых , можно использовать все способы задания (описания) функции (случайной величины), достаточно подробно изложенные в элементарных курсах теории функций вещественной (табличный, аналитический, графический и др.). Если же состоит не из чисел, то возникают проблемы задания случайных величин как вещественных функций от элементарных событий. Мы ограничимся заданием случайной величины с помощью явного указания соответствий между элементарными событиями и вещественными числами, если конечное множество. Этот способ задания случайной величины по существу совпадает с табличным способом ее задания.

До сих пор случайная величина ничем не отличается от обычной функции из математического анализа. Для изучения случайных величин с вероятностной точки зрения необходимо знать о том, как часто встречаются значения случайной величины. Для этого вводятся события вида , где множество , и изучаются их вероятности.

Определение. Пусть множество и случайная величина. Событие

называется попаданием случайной величины в множество .

Другими словами, событие состоит из всех элементарных событий , для которых попадает в множество .

В серьезных курсах математического анализа множества называют прообразами множества для функции . Считается, что .

Если множество это промежуток (их всего 9 видов), то вместо обозначения применяются часто следующие естественные обозначения:

, ; , ;

, ; , ;

, ;

, ;

, ;

, ;

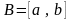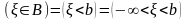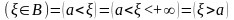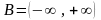, (единственный промежуток , для которого событие явно указывается для любой случайной величины ).

Определение. Пусть множество 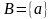и случайная величина. Событие

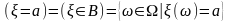
называется попаданием случайной величины в точку (число) .

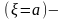Ясно, что . Поэтому событие это частный случай события .

Теорема 11.1 (основные свойства событий вида ). Верны утверждения:

1)если 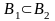, то ;

2) ;

3) ;

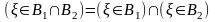4) ;

5) 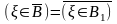, где ;

6) , где ;

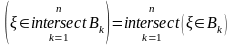7) , где ;

8) если 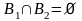, то ;

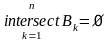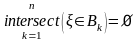9)если , то , где ;

Естественным образом возникает следующая задача, которую можно назвать основной задачей теории элементарного курса теории случайных величин.

Задача. Найти вероятность попадания случайной величины в промежуток , т.е. вероятность (одна пара скобок опускается).

Необходимо предположить, что мы изучаем такие случайные величины

, для которых события попадают в выбранную алгебру событий для любого промежутка , так как вероятность события была введена только для событий, входящих в .

Пример.

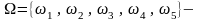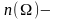Пусть пространство элементарных событий. Для всех событий вводится классическая вероятность , где количество элементов множества (события) , а количество элементов множества (события) . Случайная величина определяется так (табличный способ задания):

, , , , .

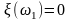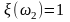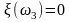Используя определение случайной величины, найти вероятности 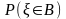попадания случайной величины в множество , если:

а) 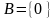; б) ; в) .

Решение.

a) .

Событие , так как и , а , и .

.

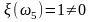б) .

Событие

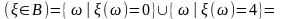
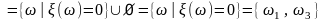, так как в множестве только ноль является значением случайной величины .

.

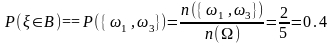в) .

Событие , так как на множестве только ноль и единица является значениями случайной величины .

.
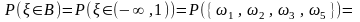