2.2. Энергетикалық спектрдің а санына тәуелділігін анықтау

Ядроны кванттық механикалық жүйе деп қарастыратын болғандықтан, ядродағы нуклондардың әсерлесу потенциалын феноменологиялық параболалы потенциалы (2.9) өрнекте анықталды. Енді осы гамильтонианның меншікті мәнін қалай есептеуді қарастырайық. Ол үшін Шредингер теңдеуін (ШТ) жазайық:

. (2.10)

Келешектегі есептеулерге қолайлы болу үшін:

белгілеулерін енгізейік. Осы белгілеулерді ескере отырып, (2.10) ШТ:

(2.11)

түрінде жазылады. Толқын функциясын тәуелсіз бір өлшемді үш осциллятордың толқын функцияларының көбейтіндісі ретінде алуға болады немесе:

.

Сонда біздің есебіміз бір өлшемді осциллятордың меншікті мәнін табуға көшеді:

. (2.12)

Бұл екінші дәрежелі дифференциал теңдеу. Осы теңдеудің толқындық функциясын және гамильтонианның меншікті мәнін қалай есептеуді көрсетейік. Толқындық функция:

а) кемімелі;

б) нормаланған немесе:

(2.13)

физикалық шарттарды қанағаттандыруы қажет. Осы физикалық шарттарды қанағаттандыратын толқындық функцияны:

(2.14)

түрінде іздейміз. Мұндағы А- нормалдау коэффициенті, В- әсерлесу интенсивтігін сипаттайтын параметр. Осы толқын функциясын Шредингер теңдеуіне (2.12) қойып, ықшамдаулардан кейін параметр В және гамильтонианның меншікті мәнін анықтаймыз. Сонда:

В=Ω; .

Сонымен (2.12) негізгі күйдегі теңдеудің шешімін:

(2.15)

түрінде анықтадық. Нормалау коэффициентін (2.13) шартынан табамыз. Ал, енді қоздырылған күйдегі теңдеудің шешімін табу керек. Оны табу үшін каноникалық айнымалыларды қарастырамыз. Ол үшін каноникалық айнымалылар, яғни импульс және координатты туу және жою операторларымен өрнектейміз

(2.16)

немесе туу , жою операторларын

(2.17)

деп анықтаймыз. Егер негізгі күйдің толқын функциясын -деп белгілесек, жою операторының әсері: болып анықталады. (2.16) өрнекті пайдаланып, (2.12) теңдеудегі гамильтонианды:

(2.18)

түрінде жазамыз. Ықшамдаулардан кейін энергетикалық спектрді нормалау шартын пайдаланып табуға болады:

. (2.19)

Қоздырылған күйдің толқын функциясын негізгі күйдің толқын функциясына туу операторының әсерінің нәтижесінде анықтаймыз, сонда:

, (2.20)

мұндағы − негізгі күйдің нормаланған толқын функциясы:

(2.21)

деп өрнектеледі. (2.20) өрнектен қоздырылған күйдің толқын функциясын анықтау үшін негізгі күйдің толқын функциясына туу операторының әсерін анықтауымыз керек. Ол үшін (2.17) өрнекке сай негізгі күйдің толқын функциясынның туындысын анықтайық:

. (2.22)

(2.17) өрнекті ескеріп, туу операторының әсерін анықтаймыз:

. (2.23)

Осы қатынасты пайдалана отырып, қоздырылған күйдің толқын функциясын анықтаймыз:

(2.24)

Сонда қоздырылған күйдің толқын функциясы:

, (2.25)

болып анықталады. Осы өрнектегі негізгі күйдің толқын функциясының орнына -ді қойсақ, қоздырылған күйдің толқын функциясы:

, (2.26)

деп жазылады, мұндағы - Эрмит полиномы:

. (2.27)

Нормалау коэффициенті:

(2.28)

болып анықталады. Сонда нормаланған қоздырылған күйдің толқын функциясы:

(2.29)

деп анықталады. Енді, - қоздырылған күйдің энергетикалық спектрін:

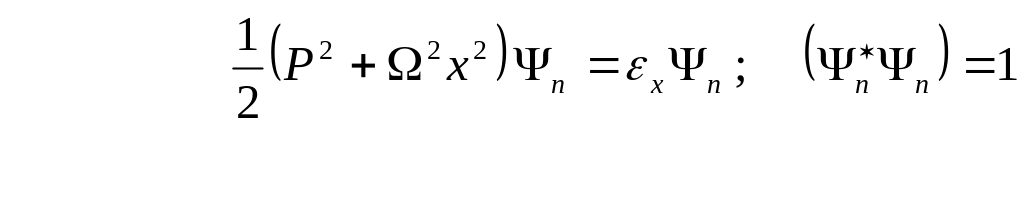(2.30)

деген нормалау шартынан анықтаймыз. Сонда:

(2.31)

Ары қарай туу және жою операторларының өрнегін пайдаланып, шаманы

деп анықтайық. Осы анықтаған шаманы (2.31) қойсақ, энергетикалық спектр

(2.32)

деп өрнектеледі. Айнымалыларға деген түрлендіру енгізсек, энергияның мәні

(2.33)

деп жазылады. Эрмит полиномының:

реккуренттік қатынасын

(2.35)

және (2.35) теңдеуді пайдалана отырып, қоздырылған күйдің энергетикалық спектрін:

(2.36)

деп анықтаймыз. Сонымен бірдей (2.12) өрнекке сай z және у координаттары үшін қоздырылған күйдің энергетикалық спектрі:

(2.37)

деп жазылады. Сонда үш өлшемді кеңістіктегі гармоникалық осциллятор потенциалының энергетикалық спектрі:

(2.38)

болып анықталады. Осы гармоникалық потенциалдың толқын функциясын пайдаланып, орташа квадраттық радиусты табамыз:

. (2.39)

Бұл тәжірибеден өлшенетін шамалардың бірі. Ол үшін әрбір құраушыларының квадратының орташасын табуымыз керек, яғни шаманы табайық:

. (2.40)

Мұндағы қоздырылған күйдің толқын функциясын (2.29) өрнегінен

(2.41)

анықталады. Эрмит полиномының келесі реккуренттік қатынасын пайдалана отырып,

(2.42)

орташа квадраттық радиусты есептесек

(2.43)

болады. Енді z және у құраушылары үшін:

(2.44)

деп жазылады. Сонда орташа квадраттық радиус:

. (2.45)

түрінде анықталады, ал толық энергия

(2.46)

тең болады. Егер ядроның көлемінің пішіні радиусты сфера және А нуклоннан тұрады десек, онда ораташа квадраттық радиусы

түрінде анықталады. Мұндағы орташа квадраттық радиустың тәжірибелік мәнімен теңестіріп және (2.45) өрнекті ескеріп

(2.47)

массалық А санына тәуелділігін анықтаймыз. Енді осы өрнектен -ны табатын болсақ, ол:

. (2.48)

Бұл өрнек толқын функциясының А санына тәуелділігін

(2.49)

сипаттайды. Бұл (2.49) өрнек, (2.46) өрнектен гармоникалық осциллятор потенциалының энергетикалық спектрінің А санына тәуелділігін аналитикалық тұрғыдан анықтауға мүмкіндік береді, яғни:

. (2.50)

Бұл өрнектен энергетикалық спектр бас кванттық сан N өскенде өседі, ал А саны өскенде кемитінін көруге болады. Ол тәжірибелік нәтижелермен сапалы түрде үйлеседі. Ал басқа Юкава, Буд-Саксон потенциалдары үшін энергетикалық спектрі және толқын функциясы тек сандық әдістердің көмегімен ғана анықталады.

Бақылау сұрақтары:

1. Гамильтонианның меншікті мәнін қалай анықтаймыз?

2. Ядроның орташа квадраттық радиус неге тең?

3. Туу және жою операторлары қалай анықталады?

4. Гармоникалық осциллятор потенциалы энергетикалық спектрі неге тең?

5. Энергетикалық спектрдің А санына тәуелділігі қандай?