
- •Справочный материал
- •Комплексные числа
- •Пределы
- •Непрерывность функции в точке
- •Производная Правила дифференцирования
- •5. Исследование функции и построение её графика Основные свойства функций
- •3. Выпуклость графика функции. Точки перегиба.
- •4. Асимптоты графика функции.
- •Пример решения типового задания
Справочный материал
-
Комплексные числа
Алгебраической
формой комплексного
числа
 называется выражение вида
называется выражение вида
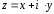 ,
где
,
где
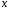 и
и
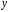 – действительные числа, а
– действительные числа, а
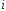 –
так называемая мнимая единица (
–
так называемая мнимая единица (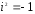 ).
).
Число
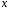 называется действительной частью
комплексного числа
называется действительной частью
комплексного числа
 (
(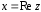 ),
число
),
число
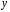 -
мнимой частью
-
мнимой частью
 (
(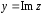 ).
).
Два
комплексных числа
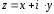 и
и
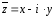 ,
отличающиеся лишь знаком мнимой части,
называются сопряженными.
,
отличающиеся лишь знаком мнимой части,
называются сопряженными.
Пусть
даны два комплексных числа
 и
и
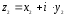 .
Они равны тогда и только тогда, когда
равны их действительные и мнимые части,
т.е.
.
Они равны тогда и только тогда, когда
равны их действительные и мнимые части,
т.е.
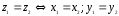 .
.
Действия над комплексными числами в алгебраической форме задаются формулами
1.
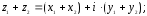
2.
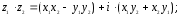
В
частности
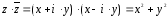 ;
;
3.
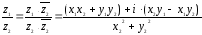 .
.
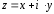 можно изобразить на плоскости
можно изобразить на плоскости
 в виде точки
в виде точки
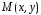 или радиус-вектора
или радиус-вектора
 .
.
 Длина
вектора
Длина
вектора
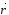 называется модулем
комплексного
называется модулем
комплексного
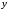



 числа
и обозначается
числа
и обозначается
 или
или
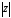 ,
а угол
,
а угол
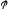 между вектором у
М
между вектором у
М


 и
положительным направлением оси
и
положительным направлением оси
 называется
называется
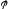
аргументом этого комплексного числа. О х х
Главным
называется
значение аргумента
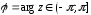 .
.
Очевидно,
что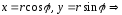
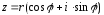 (1)
(1)
Полученная запись комплексного числа называется тригонометрической формой.
Модуль и аргумент комплексного числа определяются по формулам
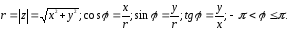
Используя
формулу Эйлера
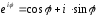
комплексное
число
 можно записать в показательной
форме
можно записать в показательной
форме
 .
.
Действия над комплексными числами в тригонометрической форме выполняются по формулам:
1.
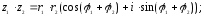
2.
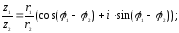
3.
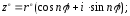 (2)
(2)
4.
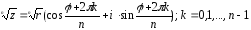 .
.
В
частности
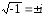 .
.
-
Пределы
Для
нахождения пределов
функции используются следующие теоремы.
Если существуют пределы
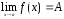 и
и
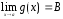 ,
то
,
то
1.
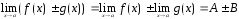 ;
;
2.
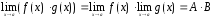 ;
;
В
частности,
 ,
где
,
где
 ;
;
3.
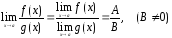 .
.
Аналогичные теоремы справедливы для пределов последовательностей.
Имеют место два замечательных предела:
1.
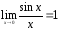 ;
2.
;
2.
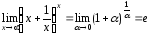 .
.
Следствия:
1.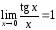 ;
2.
;
2.
 ;
3.
;
3.
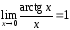 ;
4.
;
4.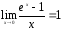
5.
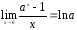 ;
6.
;
6.
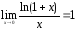 ;
7.
;
7.
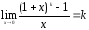 .
.
Для
раскрытия неопределённостей вида
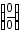 и
и
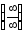 используют правило
Лопиталя.
Пусть функции
используют правило
Лопиталя.
Пусть функции
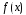 и
и
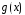 непрерывны и дифференцируемы в окрестности
точки
непрерывны и дифференцируемы в окрестности
точки
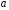 (быть может кроме неё самой);
(быть может кроме неё самой);
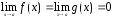 или
или
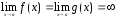 и
и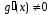 .
Тогда, если существует предел
.
Тогда, если существует предел
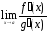 ,
то
,
то
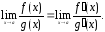 (3)
(3)
-
Непрерывность функции в точке
Функция
 называется непрерывной
в точке
называется непрерывной
в точке
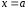 ,
если
,
если
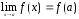 .
(4)
.
(4)
Указанное равенство предполагает, что функция определена в точке
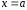 и
её окрестности и имеет предел при
и
её окрестности и имеет предел при
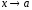 .
.
Равенство (4) эквивалентно равенству
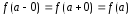 ,
(5)
,
(5)
где
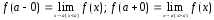 – лево и правосторонние пределы функции
в точке
– лево и правосторонние пределы функции
в точке
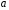 .
.
Известно, что элементарные функции непрерывны в каждой точке, в которой они определены.
Точки, в которых нарушается условие непрерывности, называются точками разрыва функции. Все точки разрыва разделяются на точки разрыва первого и второго рода.
Точка
разрыва
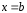 называется точкой разрыва
первого рода
функции
называется точкой разрыва
первого рода
функции
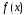 ,
если в этой точке существуют конечные
пределы слева
,
если в этой точке существуют конечные
пределы слева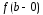 и справа и
и справа и
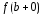 .
При этом, если
.
При этом, если
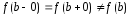 ,
то точка
,
то точка
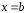 называется точкой устранимого
разрыва;
а если
называется точкой устранимого
разрыва;
а если
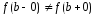 ,
то точкой конечного
разрыва.
,
то точкой конечного
разрыва.
Точка
разрыва
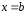 называется точкой разрыва
второго рода
функции
называется точкой разрыва
второго рода
функции
 ,
если хотя бы один из односторонних
пределов в этой точке не существует или
равен бесконечности.
,
если хотя бы один из односторонних
пределов в этой точке не существует или
равен бесконечности.
