Практичне завдання № 2
Капітал V млн. грн. може бути вкладений в банк під m % річних або інвестований у виробництво, при чому ефективність вкладення у виробництво очікується у розмірі n % в рік.
Витрати
задаються квадратичною залежністю
.
Прибуток обкладається податком в р
%. Визначити при яких р
розміщення капіталу у виробництво
вигідніше чистого вкладення капіталу
в банк.
Варіант |
V |
m |
n |
a |
1 |
1 |
20 |
140 |
5 |
2 |
21 |
40 |
180 |
40 |
3 |
9 |
8 |
80 |
40 |
4 |
7 |
5 |
110 |
20 |
5 |
2 |
68 |
140 |
25 |
6 |
6 |
17 |
80 |
50 |
7 |
3 |
30 |
100 |
16 |
8 |
2 |
20 |
200 |
4 |
9 |
2 |
20 |
100 |
10 |
10 |
5 |
22 |
70 |
15 |
Практичне завдання № 3
Підприємство випускає та реалізує продукцію в обсязі Q у. о. Функції витрат C(Q) та цін P(Q) мають вигляд:
C(Q) = aQ3 + bQ2 + cQ + d, P(Q) = AQ+ B.
Знайти:
А) максимальний прибуток підприємства, обсяг та ціну, що відповідає максимальному прибутку;
Б) середні та граничні витрати, що відповідають максимальному прибутку;
В) участки зростання та убування прибутку на відрізку [m, n];
Г) найменше значення витрат на відрізку [m, n].
Варіант |
a |
b |
c |
d |
A |
B |
m |
n |
1 |
0,8 |
-1,8 |
-6 |
120 |
-0,6 |
66 |
1 |
8 |
2 |
0,96 |
2,16 |
1,44 |
10 |
-0,72 |
44,64 |
2 |
5 |
3 |
0,5 |
1,125 |
-1,5 |
4,5 |
-1,125 |
25,5 |
1 |
6 |
4 |
0,4 |
-0,3 |
-6 |
15 |
-0,3 |
24 |
3 |
7 |
5 |
0,7 |
1,575 |
-2,1 |
25,2 |
-0,525 |
48,3 |
2 |
6 |
6 |
0,6 |
-0,45 |
-5,4 |
12,4 |
-1,35 |
30,6 |
1 |
6 |
7 |
0,4 |
-0,6 |
-4 |
85 |
-0,4 |
27 |
1 |
5 |
8 |
0,85 |
0,8 |
-6,5 |
37 |
-1,25 |
28,5 |
2 |
7 |
9 |
0,72 |
2,2 |
1,1 |
12,2 |
-0,51 |
45,5 |
3 |
6 |
10 |
0,45 |
1,5 |
-4,2 |
6,5 |
-0,42 |
22 |
1 |
8 |
Практичне завдання № 4
Знайти границю використовуючи еквівалентності, правіло Лопіталя та методи розкриття невизначеностей.
Варіант
1.
.
Варіант
2.
.
Варіант
3.
.
Варіант
4.
.
Варіант
5.
.
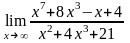Варіант
6.
.
Варіант
7.
.
Варіант
8.
.
Варіант
9.
.
Варіант
10.
.
Практичне завдання № 5
Знайти границю використовуючи методи розкриття невизначеностей.
Варіант
1.
.
Варіант
2.
.
Варіант
3.
.
Варіант
4.
.
Варіант
5.
.
Варіант
6.
.
Варіант
7.
.
Варіант
8.
.
Варіант
9.
.
Варіант
10.
.
Практичне завдання № 6
Знайти невизначений інтеграл. Результат перевірити диференціюванням.
Варіант
1.
.
Варіант
2.
.
Варіант
3.
.
Варіант
4.
.
Варіант
5.
.
Варіант
6.
.
Варіант
7.
.
Варіант
8.
.
Варіант
9.
.
Варіант
10.
.
Практичне завдання № 7
Обчислити визначені інтеграли.
Варіант
1.
.
Варіант
2.
.
Варіант
3.
.
Варіант
4.
.
Варіант
5.
.
Варіант
6.
.
Варіант
7.
.
Варіант
8.
.
Варіант
9.
.
Варіант
10.
.
Практичне завдання № 8
Варіант 1.
Варіант 2.
Варіант 3.
Варіант 4.
Варіант 5.
Варіант 6.
Варіант 7.
Варіант 8.
Варіант 9.
Варіант 9.
Практичне завдання № 8
Варіант 1. В лотереї із 100 білетів виграшними є 1 білет в 75 гривен, 4 білети в 35 гривен та 5 білетів по 15 гривен. Для випадкової величини Х – вартості можливого виграшу для власника одного лотерейного білету знайти:
А) закон розподілу;
Б) функцію розподілу;
В) математичне очікування, дисперсію та середнє квадратичне відхилення.
Варіант 2. В лотереї із 200 білетів виграшними є 5 білетів в 100 гривен, 10 білети в 50 гривен та 5 білетів по 20 гривен. Для випадкової величини Х – вартості можливого виграшу для власника одного лотерейного білету знайти:
А) закон розподілу;
Б) функцію розподілу;
В) математичне очікування, дисперсію та середнє квадратичне відхилення.
Варіант 3. В лотереї із 150 білетів виграшними є 2 білети в 50 гривен, 6 білетів в 25 гривен та 10 білетів по 20 гривен. Для випадкової величини Х – вартості можливого виграшу для власника одного лотерейного білету знайти:
А) закон розподілу;
Б) функцію розподілу;
В) математичне очікування, дисперсію та середнє квадратичне відхилення.
Варіант 4. В лотереї із 300 білетів виграшними є 10 білетів в 150 гривен, 15 білети в 75 гривен та 8 білетів по 50 гривен. Для випадкової величини Х – вартості можливого виграшу для власника одного лотерейного білету знайти:
А) закон розподілу;
Б) функцію розподілу;
В) математичне очікування, дисперсію та середнє квадратичне відхилення.
Варіант 5. В лотереї із 50 білетів виграшними є 1 білет в 25 гривен, 2 білети в 15 гривен та 4 білети по 10 гривен. Для випадкової величини Х – вартості можливого виграшу для власника одного лотерейного білету знайти:
А) закон розподілу;
Б) функцію розподілу;
В) математичне очікування, дисперсію та середнє квадратичне відхилення.
Варіант 6. В лотереї із 400 білетів виграшними є 15 білетів в 300 гривен, 25 білети в 150 гривен та 45 білетів по 50 гривен. Для випадкової величини Х – вартості можливого виграшу для власника одного лотерейного білету знайти:
А) закон розподілу;
Б) функцію розподілу;
В) математичне очікування, дисперсію та середнє квадратичне відхилення.
Варіант 7. В лотереї із 500 білетів виграшними є 5 білет в 1000 гривен, 10 білетів в 500 гривен та 20 білетів по 250 гривен. Для випадкової величини Х – вартості можливого виграшу для власника одного лотерейного білету знайти:
А) закон розподілу;
Б) функцію розподілу;
В) математичне очікування, дисперсію та середнє квадратичне відхилення.
Варіант 8. В лотереї із 500 білетів виграшними є 5 білетів в 1500 гривен, 15 білетів в 1000 гривен та 20 білетів по 500 гривен. Для випадкової величини Х – вартості можливого виграшу для власника одного лотерейного білету знайти:
А) закон розподілу;
Б) функцію розподілу;
В) математичне очікування, дисперсію та середнє квадратичне відхилення.
Варіант 9. В лотереї із 50 білетів виграшними є 1 білет в 50 гривен, 2 білети в 25 гривен та 3 білетів по 15 гривен. Для випадкової величини Х – вартості можливого виграшу для власника одного лотерейного білету знайти:
А) закон розподілу;
Б) функцію розподілу;
В) математичне очікування, дисперсію та середнє квадратичне відхилення.
Варіант 10. В лотереї із 75 білетів виграшними є 3 білети в 120 гривен, 6 білетів в 55 гривен та 12 білетів по 30 гривен. Для випадкової величини Х – вартості можливого виграшу для власника одного лотерейного білету знайти:
А) закон розподілу;
Б) функцію розподілу;
В) математичне очікування, дисперсію та середнє квадратичне відхилення.