§ 5. Геометрический смысл производной

Ррисунок 9.

Производная функции представляет собой угловой коэффициент касательной, проведенной к графику функции в любой его точке (рис.9).

Угловой коэффициент касательной, проведенной к графику функции в точке М₀(х₀;у₀) равен значению производной функции при :

Касательной к графику функции в точке М₀(х₀;у₀) называется прямая, задаваемая уравнением:

или

Пример 1 . Найти угловой коэффициент касательной к кривой в точке .

Решение: Тогда согласно геометрическому смыслу производной .

Ответ:

Ответ: =2

Пример 2 . Составить уравнение касательной, проведенной к кривой

в точке с абсциссой .

Решение: Уравнение касательной .

1. Найдем ординату точки касания (подставляем в уравнение кривой 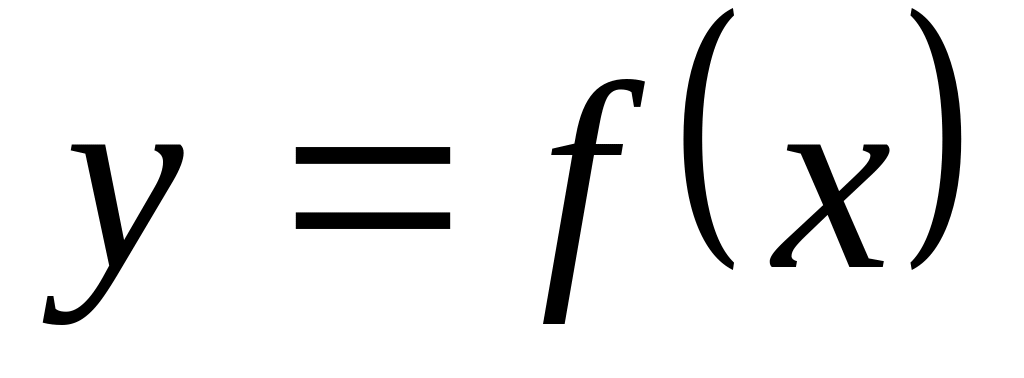значение абсциссы 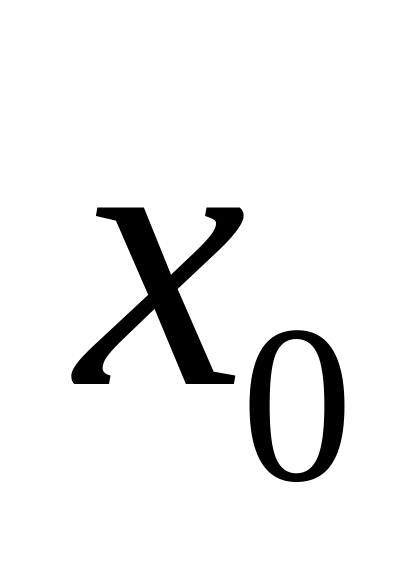): 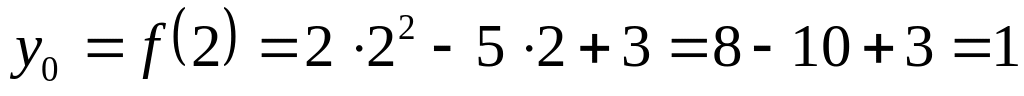; Запишем координаты точки касания 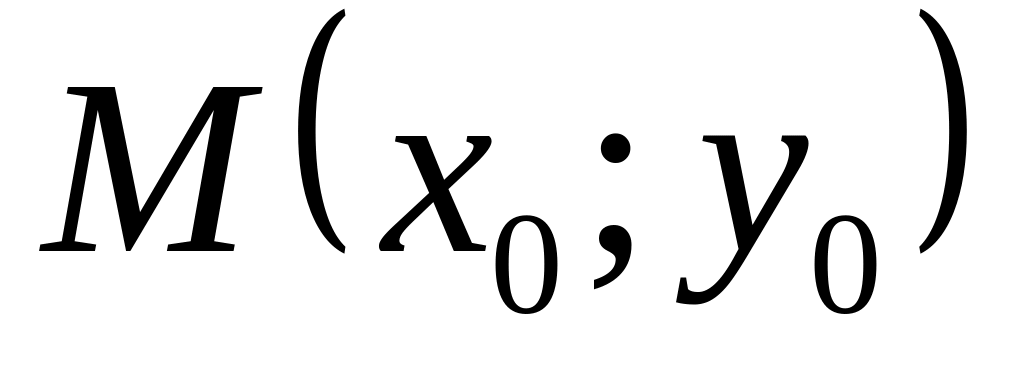: М(2; 1);

2. Определим угловой коэффициент касательной (находим производную 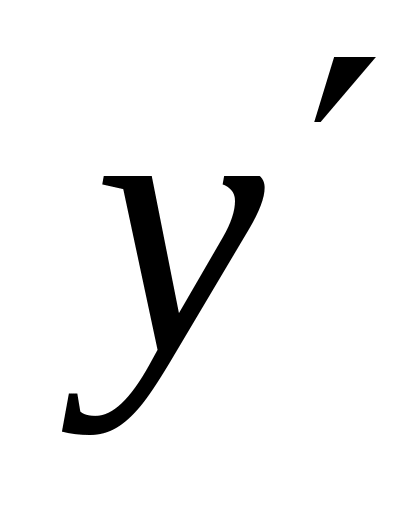и вычисляем ее значение при ):

. Итак, .

3. Подставим в уравнение касательной координаты точки касания и значение углового коэффициента касательной:

.

Ответ: Уравнение касательной .

§ 6. Физический смысл производной. Вторая производная и ее физический смысл

Определение 1. Производная пути по времени равна скорости движения тела в данный момент времени t:

Быстрота протекания физических, химических и других процессов также выражается с помощью производной.

Определение 2. Производная функции равна скорости изменения этой функции при данном значении аргумента х: .

Определение 3. Производной второго порядка (или второй производной)

функции называется производная от первой производной: или .

Пример 1. Найти вторую производную функции .

Решение: Сначала по формуле найдем первую производную:

.

Дифференцируя еще раз по формулам ,

найдем вторую производную:

.

Ответ: .

Определение 4. Производная скорости по времени t (или вторая производная пути по времени) равна ускорению движения тела в данный момент времени t:

Пример 2. Точка движется прямолинейно по закону . Найти значения скорости и ускорения в момент времени с.

Решение:

1) Найдем скорость движения точки в любой момент времени (как производную пути по времени): .

2) Вычислим скорость движения точки в момент времени с:

. 3) Найдем ускорение движения точки:

4) Вычислим ускорение движения точки в момент времени с:

Ответ: ,

Пример 3. Зависимость пути от времени при прямолинейном движении точки задана уравнением . В какой момент времени ускорение движения ?

Решение: 1) Найдем скорость движения точки в любой момент времени

.

2) Найдем ускорение движения точки:

3) Из условия найдем момент времени : .

Ответ: В момент времени с. ускорение движения .