
- •Тема 4. Введение в анализ
- •§1. Функции одной переменной
- •Вопрос 1. Основные подмножества (промежутки) расширенной числовой прямой
- •Основные подмножества (промежутки) расширенной числовой прямой
- •Окрестность точки
- •Вопрос 2. Понятие функции, способы задания функций
- •Способы задания функции
- •Вопрос 3. Основные характеристики функций Четность(нечетность)
- •Монотонность
- •Ограниченность
- •Периодичность
- •Вопрос 4. Сложная и обратная функции Обратная функция
- •Сложная функция (суперпозиция функций)
- •Вопрос 5. Основные элементарные функции
- •Основные элементарные функции
Вопрос 3. Основные характеристики функций Четность(нечетность)
О.3.1.Функция y = f(x), определенная на множестве Х, называется четной (нечетной), если:
1) для любого xX xX (множество Х симметрично относительно 0);
2) f(x) = f(x) (f(x) = f(x)).
График четной функции симметричен относительно оси Оу, а нечетной – относительно начала координат.
Монотонность
О.3.2.Функция y = f(x) называется возрастающей (неубывающей) на промежутке Х, если для любых x1, х2X из того, что x1 < х2 следует, что f(x1) < f(x2) (f(x1) f(x2)).
О.3.3.Функция y = f(x) называется убывающей (невозрастающей) на промежутке Х, если для любых x1, х2X из того, что x1 < х2 следует, что f(x1) f(x2) (f(x1) f(x2)).
Возрастающие, невозрастающие, убывающие, неубывающие функции на множестве Х называются монотонными на этом множестве, а возрастающие и убывающие функции называются строго монотонными.
Ограниченность
О.3.4. Функция y = f(x) называется ограниченной на множестве Х, если существует такое число М>0, что для любого хХ: f(x) М.
Пример 3.
y = sin x - ограниченная функция (sin x 1).
у = х2 - ограниченная снизу функция (х2 0).
у = х2 - ограниченная сверху функция (х2 0).
Периодичность
О.3.5. Функция y = f(x), определенная на множестве Х, называется периодической на этом множестве, если существует такое число Т>0, что для любого хХ: (х + Т)Х и f(x + Т) = f(x). Число Т называется периодом функции.
Т.3.1. Если функция y = f(x) имеет период Т, то и любое число вида kT (kZ) так же является ее периодом.
Пример 4. y = sin x Т = 2k (kZ).
Вопрос 4. Сложная и обратная функции Обратная функция
Пусть функция y = f(x) определена на множестве Х и имеет множество значений У.
О.4.1.Если каждому значению
![]() соответствует единственное значение
соответствует единственное значение
![]() ,
то определена функция
,
то определена функция
![]() с областью определения У и множеством
значений Х. Такая функция
называется обратной к функции y
= f(x).
с областью определения У и множеством
значений Х. Такая функция
называется обратной к функции y
= f(x).
Про функции y = f(x) и говорят, что они являются взаимно обратными.
Если использовать стандартные обозначения, то обратную функцию можно записать в виде
![]() .
.
Пример 5. Функции
![]() и
и
![]() являются взаимно обратными.
являются взаимно обратными.
Графики взаимно обратных функций y
= f(x) и
![]() симметричны относительно биссектрисы
I и III
координатных углов.
симметричны относительно биссектрисы
I и III
координатных углов.
Сложная функция (суперпозиция функций)
Пусть даны функции:
1)
![]() с областью определения U и множеством
значений У;
с областью определения U и множеством
значений У;
2)
![]() с областью определения Х и множеством
значений
с областью определения Х и множеством
значений
![]() ,
причем
,
причем
![]() .
.
О.4.2. Функция
![]() ,
заданная на множестве Х, называется
сложной функцией от х или суперпозицией
функций
,
заданная на множестве Х, называется
сложной функцией от х или суперпозицией
функций
![]() и
и
![]() .
Переменная
называется промежуточным аргументом
сложной функции.
.
Переменная
называется промежуточным аргументом
сложной функции.
Пример 6.
![]()
![]() и
и
![]() .
.
Сложная функция может иметь несколько промежуточных аргументов.
Вопрос 5. Основные элементарные функции
Наиболее простые приложения математического анализа ограничиваются кругом так называемых элементарных функций.
Основные элементарные функции
Степенная функция:
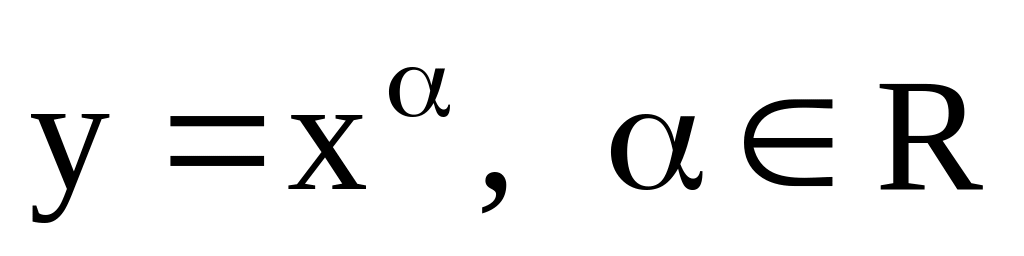 .
.Показательная функция:
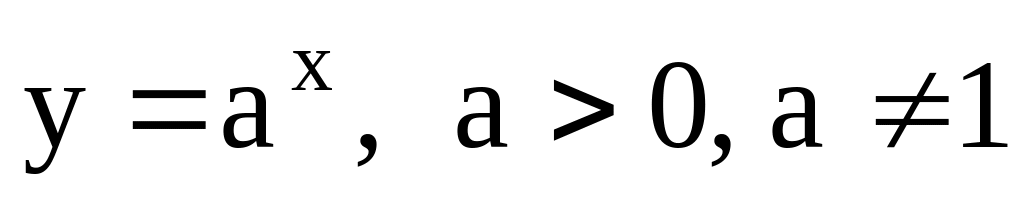 .
.Логарифмическая функция:
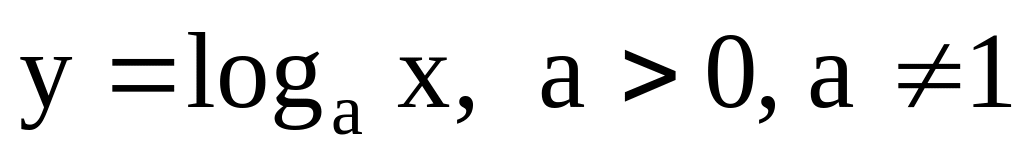 .
.Тригонометрические функции:
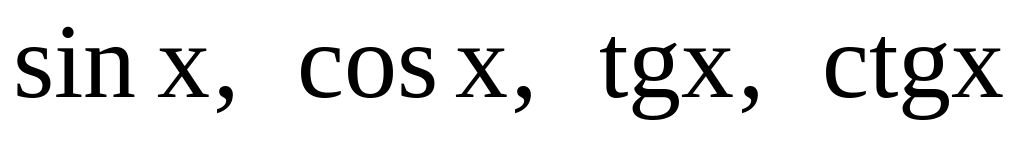 .
.Обратные тригонометрические функции:
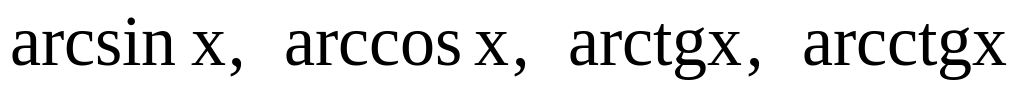 .
.
О.5.1.Элементарной функцией называется функция, которая получается из основных элементарных функций с помощью конечного числа арифметических действий (сложение, вычитание, умножение и деление) и суперпозиций.
Пример 7.
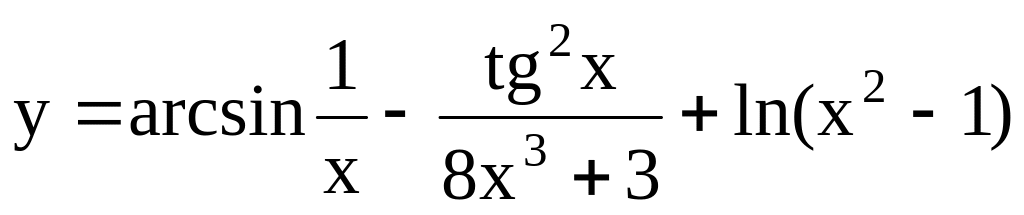 - элементарная функция.
- элементарная функция. - неэлементарная функция.
- неэлементарная функция.
