Функции распределения и их графическое представление
Помимо наибольшего, наименьшего и среднего размеров частиц более полно полидисперсность материала характеризуется дисперсным составом. Данная характеристика позволяет определить не только перечисленные параметры, но и установить процентное содержание частиц с определенным интервалом размеров.
С точки зрения математической статистики, диаметр частиц можно рассматривать как одномерную случайную величину. В этом случае свойства полидисперсного материала описывают функцией распределения числа частиц от их размера.
Как правило, процентное содержание отдельных фракций представляют в виде гистограммы – ступенчатого графика зависимости относительного содержания фракций частиц от их размера.
Гистограмму строят в виде диаграммы, состоящей из нескольких прямоугольников (их число соответствует числу фракций), основания которых находятся между значениями диаметра от di–∆di/2 до di+∆di/2 (рис. 2). Такие гистограммы дают наглядное представление о степени полидисперсности анализируемых систем и содержании в них каждой фракции, поскольку интервалы диаметров во фракциях берутся одинаковыми.
При построении дифференциальных кривых распределения частиц по размерам по оси абсцисс также отсчитываются значения их диаметров, а по оси ординат – отношение процентного содержания частиц в каком-то интервале размеров ∆Qi к этому интервалу ∆di, т.е. плотность распределения. Здесь величины интервалов размеров ∆di могут быть неодинаковыми. Дифференциальную кривую распределения частиц по размерам получают, построив на графике отдельные для каждого интервала от di–∆di/2 до di+∆di/2 прямоугольники и соединив средние точки их верхних оснований плавной кривой (рис. 3).
Для получения дифференциальной кривой численного распределения по оси ординат откладывают отношения ∆Qni/∆di. Значение численного содержания каждой фракции в процентах вычисляют по формуле:
(3)
Для построения дифференциальных кривых массового и поверхностного распределения по размерам по оси ординат наносят, соответственно, ∆Qwi/di и ∆Qsi/∆di. Значения массового и поверхностного содержания фракций в процентах рассчитывают как [4]
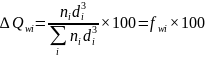(4)
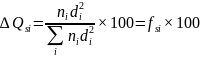(5)
Рисунок 2 - Гистограмма распределения частиц по размерам
Рисунок 3 - Дифференциальная кривая распределения частиц по размерам
Экспериментальная часть
2.1 Материалы
Хлорида кальция дигидрат, карбонат натрия, этиловый спирт. Вода, используемая во всех экспериментах, была подготовлена в трехэтапной Millipore Milli-Q 185 Plus системе очистки и имела удельное сопротивление выше, чем 18,2 MОм· см.
2.1.1 Получение микрочастиц карбоната кальция
К 2.5 мл деионизованной воды при активном перемешивании с помощью магнитной мешалки быстро прилить одновременно по 0.615 мл 1 М растворов хлорида кальция и карбоната натрия. Смесь перемешивать 30 секунд, затем суспензию образовавшихся частиц оставить на 30 секунд до полной кристаллизации карбоната кальция. Далее осадок CaCO3 необходимо промыть деионизованной водой, разделить с помощью центрифуги и удалить супернатант (жидкую фазу). Отмывку повторить 3 раза. Затем к осадку добавить этанол (или ацетон), перемешать, отцентрифугировать (5000 оборотов/мин, 10 секунд). Жидкую фазу отобрать и поместить сушиться при 50°С.